有一位数学老师問另一位音乐老师：

“音乐里只有七個音，你为什么要花一生的時間去研究呢？”

音乐老师迟疑了一下，反问道：

“数学里面不也只有十個数字，你又为何研究了一辈子还研究不清楚呢？”

人们不会否认艺术（如雕塑、建筑、绘画等）与数学的关系，因为它们需要计算。但如果说到音乐与数学的关系，就不太一样了，大多数人可能很迷惘：数学与音乐有关系吗？

其实在音乐发生的最初级阶段（上溯到毕达哥拉斯时代），它就与数学有着亲密的血缘关系。 毕达哥拉斯认为“数”是世界万物的本源，包括音阶序列（五度音或八度音）。他认为音阶更多是出于推理而不完全是人耳分辨的纯粹“自然”结果……

去年10月17日，《分形几何》之父Mandelbrot在美国麻省的家中去世。为了纪念这位杰出的数学家，此文中我们谈谈分形数学与音乐的关系。

曼德勃罗Mandelbrot原籍是波兰犹太人，1949年获得美国加州理工学院航空学硕士学位，后回到法国，于1952年在巴黎大学获得数学博士学位，之后曾经做过冯*诺伊曼的博士后。

什么是分形呢？我们在《有趣的分形龙》一文中作过一些介绍。分形之父曼德勃罗曾以"花菜"作比喻，对"分形"给出了一个非常形象的解释：

 
“这是一个菜花，一种非常普通和古老的蔬菜。尽管它很古老， 却又非常复杂，但同时也非常简单！不过，假设您想测量它的表面积，可不容易！ 您可以用一把锋利的刀， 切下其中一朵花， 观察它， 您仍然看到一棵整菜花！只是小点儿而已。 您然后再切， 再切，再切，……您得到的仍然是小菜花，只是更小，更小，更小……”

下图的曼德勃罗集就是一种最美妙的分形。

上图来源于：http://www.tianfangyetan.net/cd/java/iterfract.html

 它是用如下的非线性迭代法产生的：

 考虑复数平面上有一个初始点z0  =（0,0），（这儿将z0取在原点）

和另一个固定的常数复数：c =（cx, cy），

我们可以从z0及c算出另一个复数：z1 =（x1,y1）= z0×z0 + c，

然后，再计算z2 = z1×z1 + c，Z3 = z2×z2 + c，Z4 = z3×z3 + c，……

这样迭代地算下去，迭代n次之后，得到Zn。

考虑（n->无穷）的情况，最后的Zn会落在复数平面上的什么位置呢？它和原点的距离Rn是多大呢？不外乎两种情形：Rn->无穷，或者Rn->有限数。答案是完全由复数c决定的。也就是说，不同的c将给出不同的Rn。一部分复数c给出Rn->无穷，而另一部分复数c给出Rn->有限数。所有给出Rn->有限数的复数c的集合，构成曼德勃罗集。

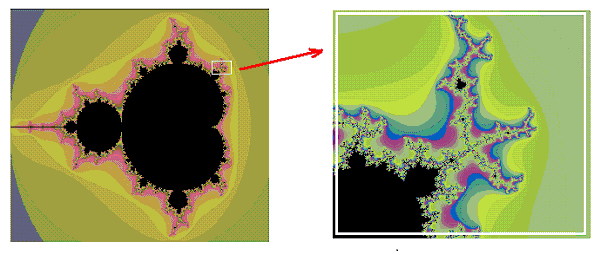
如果我们在复数平面上，将属于曼德勃罗集的点用黑色表示，将不属于曼德勃罗集的点用彩色表示，就画出了上图中的左图。

如果你使用上面连接中的曼德勃罗图程序，逐级放大，便会发现曼德勃罗集的边界有着令人吃惊的复杂结构。属于曼德勃罗集的点（黑色区域）与不属于曼德勃罗集的点（非黑色区域）以很不一般的方式混合在一起。似乎看不到一条清晰的边界。例如，将左图的曼德勃罗图右上方的一个小距形区域放大之后，我们将得到上面的右图。从右图可见：‘黑’‘白’一点也不分明，可以用一句中国人常说的话来形容:“你中有我,我中有你”，这正是分形的特征。

刚才定义曼德勃罗集时，用了‘无穷大’的概念，而在实际的数值计算程序中，这个‘无穷大’，只能用一个大得足够的数来代替。当n->无穷时，Rn的极限情况，也可以分成不只两种情形。比如说，可以按照如下方法来决定c的颜色：

如果Rn>10000，c为黑色；

如果1000>Rn>10000，c为红色；

如果500>Rn>1000，c为橙色；

如果100>Rn>500，c为黄色；

…………

也就是说，如果将Rn按大小划分成7个范围的话，我们就可以用‘红橙黄绿蓝靛紫’来分别标识它们所对应的c，得到彩色的曼德勃罗集图形。

如上所说的用迭代法产生图像的过程，也可以照样用来产生音乐！比如说，如果用‘哆唻咪法嗦啦啼’来代替‘红橙黄绿蓝靛紫’，一条时间轴代替两維复数空间中的一条线的话，一段‘分形音乐’就产生出来了！             

比如，到下列视频网站，可以欣赏更多的分形音乐（Fractal  music）:

http://www.youtube.com/watch?v=uHg_g-3Yeow&feature=related

尽管分形音乐现在听起来可能还不是那么宏伟和美妙，但至少使人觉得有趣吧，毕竟不是人，而是电脑产生出来的音乐！如果再加上一些人为的努力，使将来的‘分形音乐’更逼真地模仿真正的音乐，是完全可能的。

除了曼德尔布集之外，人们还研究了许许多多其他种类的分形，并且发现，自然界的分形现象比比皆是：从漫长蜿蜒的海岸线，到人体大脑的结构，分形似乎无所不在！这些无所不在的分形，它们有什么共同的几何特性呢？分形最重要的共同特征，是它们的自相似性。最开头我们说到的‘花菜’的例子，很直观的给出了‘自相似性’的定义：部分与整体形状相似，只是尺寸大小不同而已。

自然界中常见的分形，除了‘自相似性’之外，还表现出随机性。

当你仔细观察曼德尔布集的图形，在多次放大的过程中，你会经常见到‘似曾相识’、却又不完全相同的图景，这里的‘似曾相识’，就是来源于分形的‘自相似性’；而‘不完全相同’，则体现了曼德尔布集图形貌似随机的一面。

既然分形无处不在，当然也存在于音乐大师们所作的音乐中。听音乐时，我们不也经常听到某个旋律反复出现，然而又变化多端，并不是只作简单重复的情况吗？也许，正是这种相似性和随机性的和谐结合，你中有我，我中有你，既相似又随机，互相渗透，穿插其中，才使音乐给了我们艺术的美感，给了我们无穷想象的空间。

人们通过计算机，分析研究了音乐大师们的作品，发现分形结构，普遍存在于经典音乐作品中，比如巴赫和贝多芬的作品。

不仅仅是类似于曼德尔布集和茱莉亚集那种看起来复杂的分形存在于音乐中，更广义地说：美妙而简单的数学规律普遍存在于音乐大师们的作品中。

比如，在建筑和绘画中经常见到的黄金分割规律，也广泛存在于音乐中。

上世纪90年代，加州尔文分校的“神经生物学系记忆中心”的研究人员们，发现莫扎特的音乐对年轻孩童们，具有一种神奇的力量，可以加强注意力，提高创造力。听一段莫扎特的音乐，好比是做了一场促进协调、提高脑部功能的运动。这个结论公布之后，美国有些学校，在课堂上播放莫扎特的音乐，作为背景音乐，据说对加强课堂纪律，安抚学生情绪，起到良好作用。

莫扎特的音乐简单而纯粹，不像巴赫音乐的繁复，也不像贝多芬的使人荡气回肠。特别是莫扎特的小提琴协奏曲，单纯、明丽、幽雅而流畅。有人研究分析了几首莫扎特的小提琴协奏曲的曲式结构，发现99%都符合，或近似符合黄金分割律。用更通俗的话来说，就是曲调的重要段落所在位置，大都在整部曲子的0.613处。此外，附属主题、音调转接、主题再现、副歌开始等等，也大都相对发生于各段的黄金分割点。

也许，莫扎特的小提琴协奏曲给人的‘简单和美’的感觉，就根源于这些简单的黄金分割？

刚才介绍过现代作曲家根据分形创作的‘分形音乐’。也有人用更简单的数学规律，诸如二进制序列，各种级数，甚至一段英语文字等等，来创作音乐。用数学作曲，已经成为现代作曲家的热门课题。反正，音乐曲谱实际上也是一种编码，只要你想出一种什么方法，将数学的东西与音乐码互相转换，你就能写出一段曲子来。好听与否就是另一回事了。

 
下面是Stony Brook 一个音乐系学生根据Fibonacci数作的一小段曲，他用钢琴演奏出来：

https://docs.google.com/leaf?id=0B7ZOv_0yiMYgM2VlMDQwNTMtNDU2Yi00MWZk...