白话·场方程（4） 广相论31

亲爱的朋友，通过前面的介绍，

我们了解到，张量的实质是一种‘多重线性函数’。

或者简记为“张量的实质是函数”。

这样咱们就可以从最简单的‘基本函数’说起了。

什么是函数？

就是（通过某种规则）来‘拉关系’。

这样的解释是调侃、开个玩笑而已，

为此，请务必观看下面的视频。

或者也可记忆为、一个方程的求解过程，

就是从已知量，求未知函数的过程。

如前述，张量的实质是函数，

而函数可以用‘坐标’或用‘矩阵’来表示。

稍有数学知识的人都知道，

最简单的坐标，如下图所示：

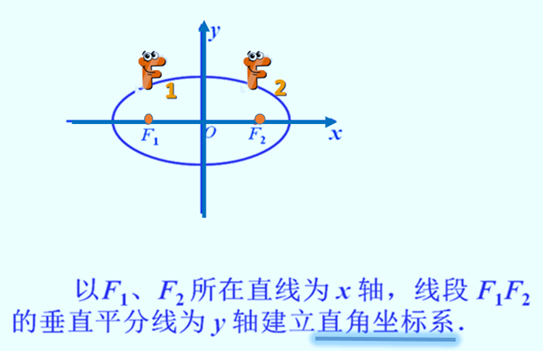
注：黎曼几何用的是曲线坐标系

（注释：用‘曲线坐标’来描述空间任意点的坐标系，      称为‘曲线坐标系’）。

 函数也可以用矩阵*来表示。

矩阵（Matrix）

是一个按照‘长方形’排列的数的集合 。

矩阵里的元素可以是数字、符号

或数学式。例如，由6个数字构成的2行3列矩阵。

大小相同的矩阵之间，可以相互加减，

具体是对每个位置上的元素，做加减法。

矩阵的乘法

（即‘点乘’或‘叉乘’），则较为复杂。

好，前面我们围绕着什么是张量，

做了最简单的介绍，但是爱因斯坦场方程

还包含度规、应力等一系列概念。

还记得我们曾介绍的场方程所含术语名称及读音吗——

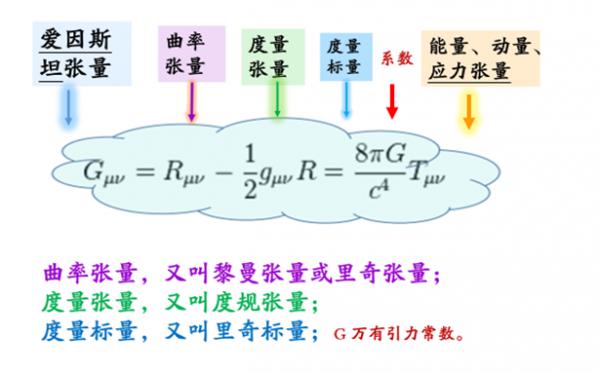
亲爱的朋友

明天我们将对上面那些术语逐项展开说明。谢谢。