有一位數學老師問另一位音樂老師：

“音樂里只有七個音，你為什麼要花一生的時間去研究呢？”

音樂老師遲疑了一下，反問道：

“數學裡面不也只有十個數字，你又為何研究了一輩子還研究不清楚呢？”

人們不會否認藝術（如雕塑、建築、繪畫等）與數學的關係，因為它們需要計算。但如果說到音樂與數學的關係，就不太一樣了，大多數人可能很迷惘：數學與音樂有關係嗎？

其實在音樂發生的最初級階段（上溯到畢達哥拉斯時代），它就與數學有着親密的血緣關係。 畢達哥拉斯認為“數”是世界萬物的本源，包括音階序列（五度音或八度音）。他認為音階更多是出於推理而不完全是人耳分辨的純粹“自然”結果……

去年10月17日，《分形幾何》之父Mandelbrot在美國麻省的家中去世。為了紀念這位傑出的數學家，此文中我們談談分形數學與音樂的關係。

曼德勃羅Mandelbrot原籍是波蘭猶太人，1949年獲得美國加州理工學院航空學碩士學位，後回到法國，於1952年在巴黎大學獲得數學博士學位，之後曾經做過馮*諾伊曼的博士後。

什麼是分形呢？我們在《有趣的分形龍》一文中作過一些介紹。分形之父曼德勃羅曾以"花菜"作比喻，對"分形"給出了一個非常形象的解釋：

 
“這是一個菜花，一種非常普通和古老的蔬菜。儘管它很古老， 卻又非常複雜，但同時也非常簡單！不過，假設您想測量它的表面積，可不容易！ 您可以用一把鋒利的刀， 切下其中一朵花， 觀察它， 您仍然看到一棵整菜花！只是小點兒而已。 您然後再切， 再切，再切，……您得到的仍然是小菜花，只是更小，更小，更小……”

下圖的曼德勃羅集就是一種最美妙的分形。

上圖來源於：http://www.tianfangyetan.net/cd/java/iterfract.html

 它是用如下的非線性迭代法產生的：

 考慮複數平面上有一個初始點z0  =（0,0），（這兒將z0取在原點）

和另一個固定的常數複數：c =（cx, cy），

我們可以從z0及c算出另一個複數：z1 =（x1,y1）= z0×z0 + c，

然後，再計算z2 = z1×z1 + c，Z3 = z2×z2 + c，Z4 = z3×z3 + c，……

這樣迭代地算下去，迭代n次之後，得到Zn。

考慮（n->無窮）的情況，最後的Zn會落在複數平面上的什麼位置呢？它和原點的距離Rn是多大呢？不外乎兩種情形：Rn->無窮，或者Rn->有限數。答案是完全由複數c決定的。也就是說，不同的c將給出不同的Rn。一部分複數c給出Rn->無窮，而另一部分複數c給出Rn->有限數。所有給出Rn->有限數的複數c的集合，構成曼德勃羅集。

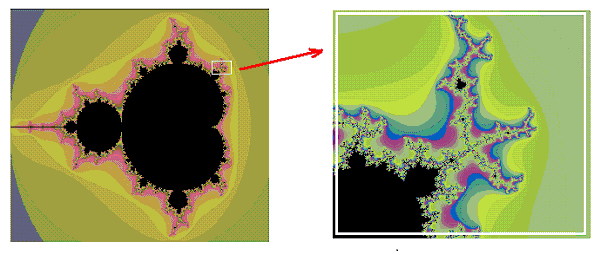
如果我們在複數平面上，將屬於曼德勃羅集的點用黑色表示，將不屬於曼德勃羅集的點用彩色表示，就畫出了上圖中的左圖。

如果你使用上面連接中的曼德勃羅圖程序，逐級放大，便會發現曼德勃羅集的邊界有着令人吃驚的複雜結構。屬於曼德勃羅集的點（黑色區域）與不屬於曼德勃羅集的點（非黑色區域）以很不一般的方式混合在一起。似乎看不到一條清晰的邊界。例如，將左圖的曼德勃羅圖右上方的一個小距形區域放大之後，我們將得到上面的右圖。從右圖可見：‘黑’‘白’一點也不分明，可以用一句中國人常說的話來形容:“你中有我,我中有你”，這正是分形的特徵。

剛才定義曼德勃羅集時，用了‘無窮大’的概念，而在實際的數值計算程序中，這個‘無窮大’，只能用一個大得足夠的數來代替。當n->無窮時，Rn的極限情況，也可以分成不只兩種情形。比如說，可以按照如下方法來決定c的顏色：

如果Rn>10000，c為黑色；

如果1000>Rn>10000，c為紅色；

如果500>Rn>1000，c為橙色；

如果100>Rn>500，c為黃色；

…………

也就是說，如果將Rn按大小劃分成7個範圍的話，我們就可以用‘紅橙黃綠藍靛紫’來分別標識它們所對應的c，得到彩色的曼德勃羅集圖形。

如上所說的用迭代法產生圖像的過程，也可以照樣用來產生音樂！比如說，如果用‘哆唻咪法嗦啦啼’來代替‘紅橙黃綠藍靛紫’，一條時間軸代替兩維複數空間中的一條線的話，一段‘分形音樂’就產生出來了！             

比如，到下列視頻網站，可以欣賞更多的分形音樂（Fractal  music）:

http://www.youtube.com/watch?v=uHg_g-3Yeow&feature=related

儘管分形音樂現在聽起來可能還不是那麼宏偉和美妙，但至少使人覺得有趣吧，畢竟不是人，而是電腦產生出來的音樂！如果再加上一些人為的努力，使將來的‘分形音樂’更逼真地模仿真正的音樂，是完全可能的。

除了曼德爾布集之外，人們還研究了許許多多其他種類的分形，並且發現，自然界的分形現象比比皆是：從漫長蜿蜒的海岸線，到人體大腦的結構，分形似乎無所不在！這些無所不在的分形，它們有什麼共同的幾何特性呢？分形最重要的共同特徵，是它們的自相似性。最開頭我們說到的‘花菜’的例子，很直觀的給出了‘自相似性’的定義：部分與整體形狀相似，只是尺寸大小不同而已。

自然界中常見的分形，除了‘自相似性’之外，還表現出隨機性。

當你仔細觀察曼德爾布集的圖形，在多次放大的過程中，你會經常見到‘似曾相識’、卻又不完全相同的圖景，這裡的‘似曾相識’，就是來源於分形的‘自相似性’；而‘不完全相同’，則體現了曼德爾布集圖形貌似隨機的一面。

既然分形無處不在，當然也存在於音樂大師們所作的音樂中。聽音樂時，我們不也經常聽到某個旋律反覆出現，然而又變化多端，並不是只作簡單重複的情況嗎？也許，正是這種相似性和隨機性的和諧結合，你中有我，我中有你，既相似又隨機，互相滲透，穿插其中，才使音樂給了我們藝術的美感，給了我們無窮想象的空間。

人們通過計算機，分析研究了音樂大師們的作品，發現分形結構，普遍存在於經典音樂作品中，比如巴赫和貝多芬的作品。

不僅僅是類似於曼德爾布集和茱莉亞集那種看起來複雜的分形存在於音樂中，更廣義地說：美妙而簡單的數學規律普遍存在於音樂大師們的作品中。

比如，在建築和繪畫中經常見到的黃金分割規律，也廣泛存在於音樂中。

上世紀90年代，加州爾文分校的“神經生物學系記憶中心”的研究人員們，發現莫扎特的音樂對年輕孩童們，具有一種神奇的力量，可以加強注意力，提高創造力。聽一段莫扎特的音樂，好比是做了一場促進協調、提高腦部功能的運動。這個結論公布之後，美國有些學校，在課堂上播放莫扎特的音樂，作為背景音樂，據說對加強課堂紀律，安撫學生情緒，起到良好作用。

莫扎特的音樂簡單而純粹，不像巴赫音樂的繁複，也不像貝多芬的使人盪氣迴腸。特別是莫扎特的小提琴協奏曲，單純、明麗、幽雅而流暢。有人研究分析了幾首莫扎特的小提琴協奏曲的曲式結構，發現99%都符合，或近似符合黃金分割律。用更通俗的話來說，就是曲調的重要段落所在位置，大都在整部曲子的0.613處。此外，附屬主題、音調轉接、主題再現、副歌開始等等，也大都相對發生於各段的黃金分割點。

也許，莫扎特的小提琴協奏曲給人的‘簡單和美’的感覺，就根源於這些簡單的黃金分割？

剛才介紹過現代作曲家根據分形創作的‘分形音樂’。也有人用更簡單的數學規律，諸如二進制序列，各種級數，甚至一段英語文字等等，來創作音樂。用數學作曲，已經成為現代作曲家的熱門課題。反正，音樂曲譜實際上也是一種編碼，只要你想出一種什麼方法，將數學的東西與音樂碼互相轉換，你就能寫出一段曲子來。好聽與否就是另一回事了。

 
下面是Stony Brook 一個音樂系學生根據Fibonacci數作的一小段曲，他用鋼琴演奏出來：

https://docs.google.com/leaf?id=0B7ZOv_0yiMYgM2VlMDQwNTMtNDU2Yi00MWZk...