| 天蓉:美妙的茱莉亞集 |
| 送交者: 天蓉 2011年12月05日07:58:04 於 [教育學術] 發送悄悄話 |
|
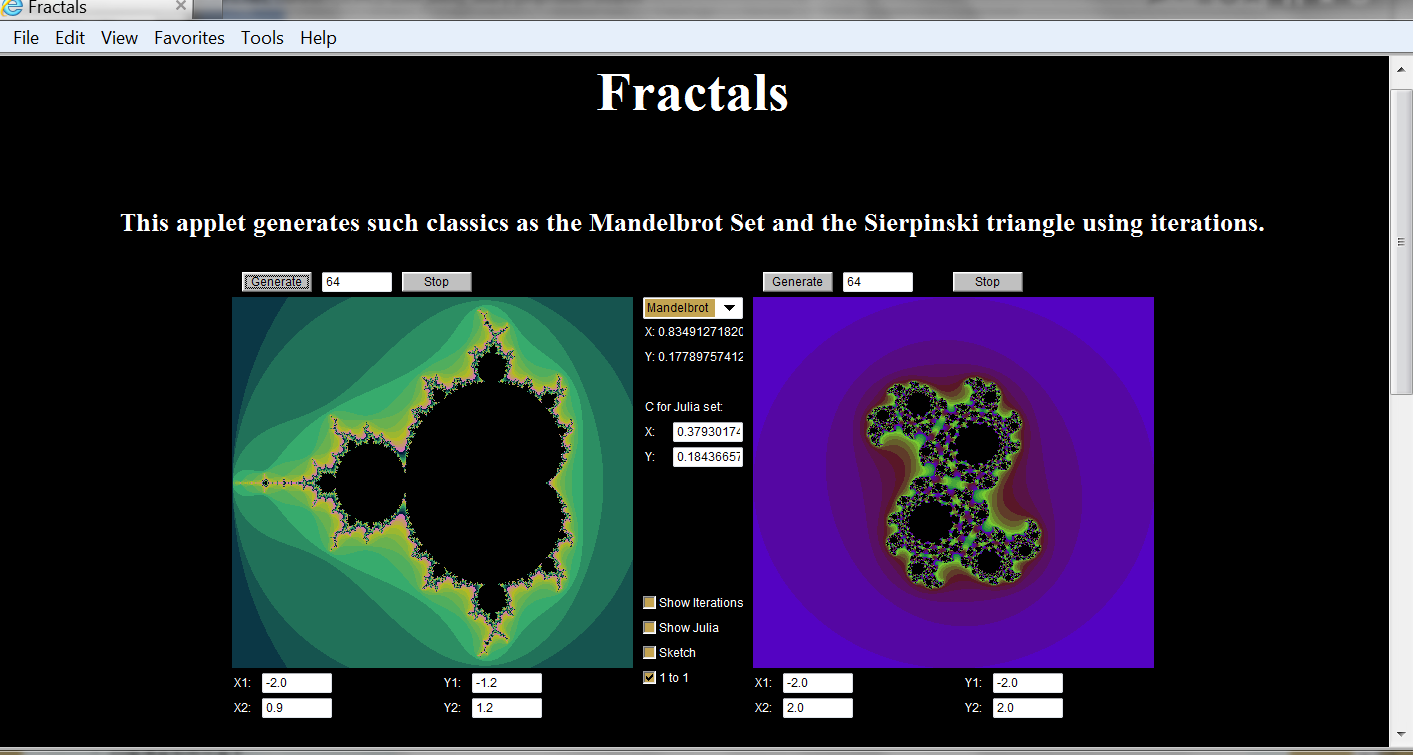
上次在《分形音樂》一文中談到過美妙的曼德勃羅集。在下列網址的曼德勃羅集的生成程序中: http://www.tianfangyetan.net/cd/java/iterfract.html 用鼠標點擊圖中左側曼德勃羅集上任何一點,或者,點擊右方的‘generate’按鈕,右側會出現一個漂亮的圖形。如果點擊左側不同的點,右側就會變化成為完全另一個不同的圖形。這些圖形和曼德勃羅集的圖形一樣:美妙非凡、變幻無窮,被人稱之為“茱莉亞集”。也就是說,茱莉亞集和曼德勃羅集的關係密切,對應於曼德勃羅集中的每一個點,都有一個茱莉亞集。 下面的圖就是從上述程序得來的,左側是曼德勃羅集,右側是對應於曼德勃羅圖形中(x=0.379,y=0.184)處的茱莉亞集。 儘管茱莉亞和曼德勃羅的名字總是連在一起,但他們卻應該算是不同時代的人。茱莉亞是法國數學家,比曼德勃羅要早上二、三十年(大約1893-1978) 。曼德勃羅直到2010年才去世。 茱莉亞年輕時參加過第一次世界大戰,一次戰鬥中被炸掉了鼻子(很可怕!他後來的照片就沒有了鼻子)。
之後,茱莉亞潛心研究數學,但其工作卻一直不被廣為人知……直到上世紀70-80年代,由曼德勃羅所奠基的分形幾何及與其相關的混沌概念被廣泛應用到各個領域之後,茱莉亞的名字才隨着曼德勃羅的名字傳播開來。這類事情在數學的發展史上屢見不鮮,就如黎曼幾何因為廣義相對論而被大家熟悉一樣。
在《分形音樂》一文中,談到過曼德勃羅集的生成方法,茱莉亞集又是如何生成的呢?
可將從曼德勃羅集而生成茱莉亞集的過程描述如下:
從茱莉亞集的生成過程可以看出:對應於曼德勃羅集中的每一個點,都有一個茱莉亞集。比如說,點擊曼德勃羅集上的零點,得到的 C值為0,這時候作上述迭代產生的茱莉亞集是單位園。
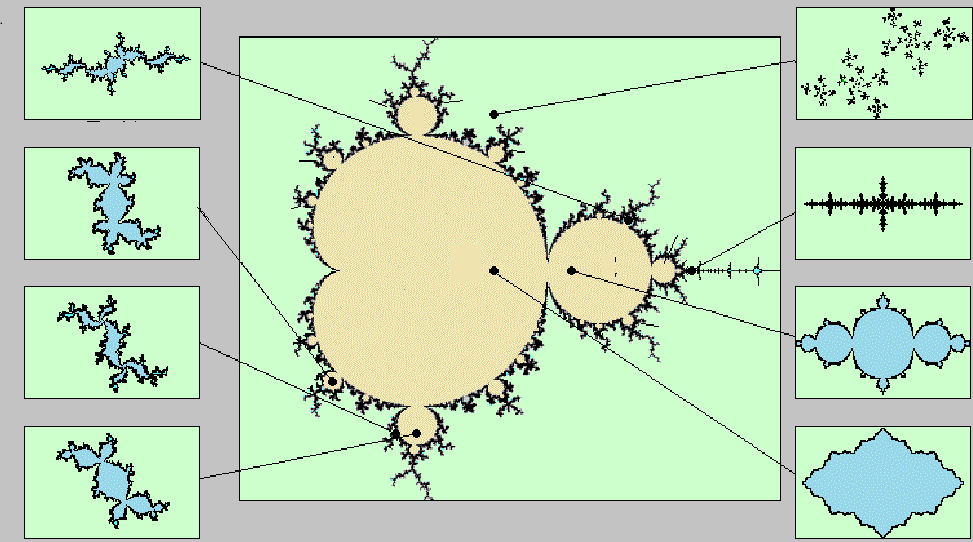
下面的圖形顯示出不同的茱莉亞集(周圍8個小圖),對應於曼德勃羅集(中間的大圖)中不同的點。
綜上所述,我們了解了美妙的曼德勃羅集和茱莉亞集圖形的產生過程。這種非線性迭代法產生的分形圖不僅僅以其神秘複雜,變化多姿受到數學及計算機愛好者們的青睞,也激勵了與此緊密相關的混沌理論及非線性動力學的發展。此外,還受到藝術家和圖案設計師們的寵愛。
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2010: | 鷹熊戀:rondeau 請achc指正 | |
| 2010: | 日行一善,替路過同學批改“鷹熊戀(ro | |
| 2009: | 中國人的標準像 | |
| 2009: | [故事] 裸 | |
| 2008: | 遠芳:零距離接觸余秋雨 | |
| 2008: | 當你年輕的時候, 想想“老”了怎麼辦 | |
| 2007: | 張維迎的管理三板斧 | |
| 2007: | 方舟子對《我和方舟子分手決裂的前前後 | |
| 2006: | 鄒承魯院士:一個良知走了 | |
| 2006: | 從工人到大學校長 華裔博士將執掌美最 | |