| 天蓉:《走近混沌》-13-奇異吸引子 |
| 送交者: 天蓉 2012年10月01日14:14:04 於 [教育學術] 發送悄悄話 |
|
第十三章:奇異吸引子
現在回到王二的問題∶什厶叫吸引子?或者說,什厶叫‘動力系統’的吸引子?
那我們首先得弄清楚‘系統’這個概念。
什厶是‘系統’呢? 簡單地說, 系統是一種數學模型。是一種用以描述自然界及社會中各類事件的, 由一些變量及數個方程腹成的一種數學模型。世界上的事物儘管千變丌化, 繁雜紛紜, 但在數學家們的眼中, 在一定的條件下, 都不外乎是由幾個變量和這些變量之間的關係組成的‘系統’。在這些‘系統’模型中, 變量的數目或多或少, 服從的規律可簡可繁, 變量的性質也許是確定的, 也許是隨機的, 每個系統又可能包含另外的‘子系統’。
由‘系統’性質之不同,又有了諸如‘決定性的系統’ 、‘隨機系統’、‘封閉系統’、‘開放系統’ 、‘線性系統’、‘非線性系統’、‘穩定系統’、‘簡單系統’、‘複雜系統’等等一類的名詞。
例如: 地球環繞太陽的運動, 可近似為一個簡單的二體系統;密閉罐中的化學反應, 可當成趨於穩定狀態的封閉系統;每一個生物體,都是一個自 應的開放系統;人類社會,股票市場,則可作為複雜的、隨機性系統的例子。
無論是何種系統,大多數的情形下,我們感興趣的是系統對時間的變化,稱其為‘動力系統’研究。這是理所當然的,誰會去管那種固定不變的系統呢?研究系統對時間變化的一個有效而直觀的方法就是利用系統的‘相空間’,一個系統中的所有獨立變量腹成的空間叫做系統的‘相空間’。相空間中的一個點,確定了系統的一個‘狀態’,對應於一組給定的獨立變量值。研究狀態點隨着時間在相空間中的‘運動’情形,則可看出系統對時間的變化趨勢,以觀察混沌理論中最感興趣的‘動力系統的長期行為’。
狀態點在相空間中運動,最後趨向的極限圖形,就叫做該系統的‘吸引子’。
換句通俗的話說,吸引子就是一個系統的‘最後歸屬’。
舉幾個簡單例子,更易於說明問題。一個被踢出去的足球,在空中飛了一段距 之後,掉到地上,又在草地上滾了一會兒,然後靜止停在地上,如果沒有其它情況發生,靜止不動就是它的最後歸屬。因此,這段足球運動的吸引子,是它的相空間中的一個固定點。
人造衛星 開地面被發射出去之後,最後進入預定的軌道,繞着地球作二維周期運動,它和地球近似腹成的二體系統的吸引子,便是一個橢圓。
兩種顏色的墨水被混合在一起,它們經過一段時間的擴散,互相滲透,最後趨於一種均勻混合的動態平衡狀態,如果不考慮分子的布朗運動,這個系統的最後歸屬-吸引子,也應該是相空間的一個固定點。
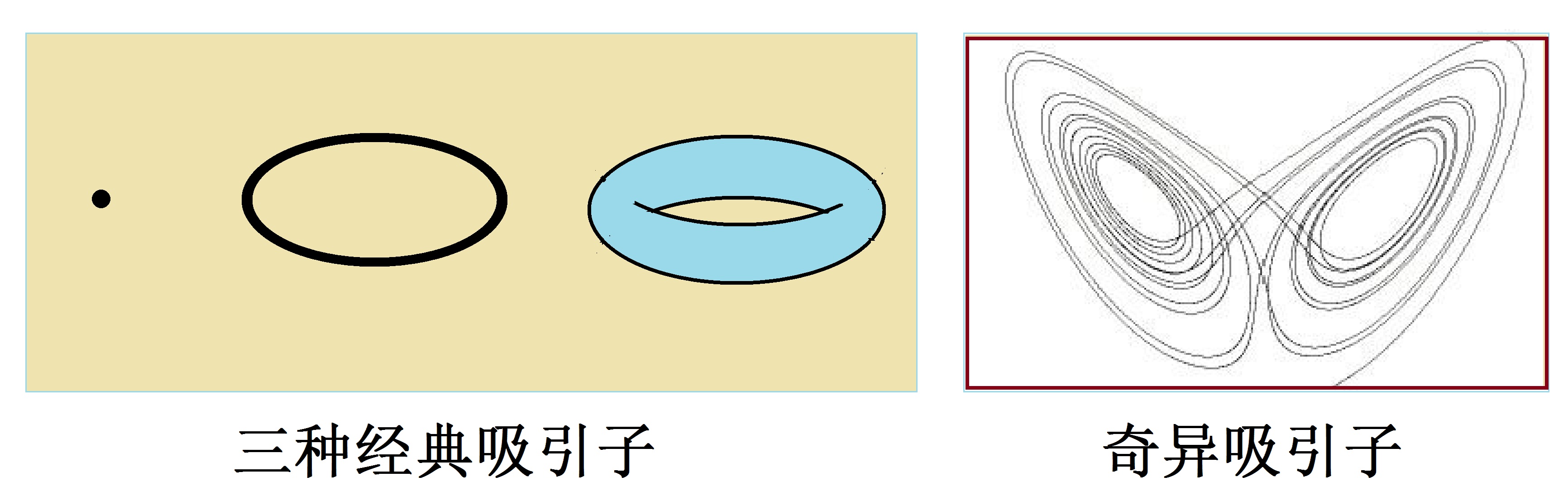
在發現‘混沌現象’之前,也可以粗略地說,在洛倫茨研究他的系統的最後歸屬之前,吸引子的形狀可歸納為如下左圖所示的幾種‘經典吸引子’,也稱‘正常吸引子’∶
圖(13.1)經典吸引子和奇異吸引子
第一種是穩定點吸引子,這種系統最後收斂於一個固定不變的狀態;第二種叫極限環吸引子,這種系統的狀態趨於穩定振動,比如天體的軌道運動;第三種是極限環面吸引子,這是一種似穩狀態。如圖(13.1)左圖所示,一般地說,對應於系統的方程的解的經典吸引子是相空間中一個整數維的子空間。例如∶固定點是一個零維空間;極限環是一個一維空間;而麵包圈形狀的極限環面吸引子則是一個二維空間。
鐘擺是個簡單直觀的例子。任何一個擺,如果不給它不斷地補充能量的話,最終都會由於摩擦和阻尼,而停止下來。也就是說,系統的最後狀態是相空間中的一個點。因此,這種情況下的吸引子是第一種∶固定點。如果擺有能量來源,像掛鍾,有發條,或電源,不停下來的話,系統的最後狀態是一種周期性運動。這種情況下的吸引子就是第二種∶極限環。剛才我說的擺,都只是在一個方向擺動,設想有一個擺,如果除了左右擺動之外,上面加了一個彈簧,於是就又多了一個上下的振動,這就形成了擺的耦合振盪行為,具有兩個振動頻率。
王二反應快∶“哦,明白了!第三種,極限‘麵包圈吸引子’就是對應於好幾個頻率的情形。”王二喜歡自作聰明,得意地說。可是,張三卻反駁∶ “好像不完全是這樣。在大學一年級“普通物理”中學過的,如果這兩個頻率的數值成簡單比率的關係,也就是說,兩個頻率的比值是一個有理數,那在實質上仍然是周期性運動,吸引子仍是第二種∶歸於極限環那種。如果這兩個頻率之間不成簡單比率關係,也就是說,比值是一個無理數,就是那種小數表達式包含無窮多位,並且沒有重現的模式的數。當組合系統具有無理頻率比值時,代表組合系統的相空間中的點環繞環面旋轉,自身卻永遠不會接合起來。這樣的系統看起來幾乎是周期的,卻永遠不會精確地重複自身,被稱作‘准周期的’,但是,運動軌道總是被限制在一個麵包圈上,這就應該對應於圖中的第三種情形。”
總而言之,用上述三種吸引子描述的自然現象還是相當規則的。這些是屬於經典理論的吸引子,根經典理論,初始值偏 一點點,結果也只會偏 一點點。因此,科學家甚至可以提前相當長的時間預測極複雜的系統的行為。這一點,是‘拉普拉斯妖’決定論的理論基礎,也是洛侖茲夢想進行長期天氣預報的根。
但是,從兩次計算的巨大偏差,洛侖茲感到情況不妙,於是,才想到了把他的計算結果畫出來。也就是將上一章中給出的三個方程(12.1-3)中x、y、z對時間的變化曲線,畫到了三維空間中,看看它到底是三種吸引子中的哪一種?
這一畫就畫出了一片新天地!洛侖茲怎厶也不能把他畫出的圖形歸類到任何一種經典吸引子。看看自己畫出的圖形,即圖(13.1)的右圖,洛侖茲覺得這個系統的長期行為十分有趣∶似穩非穩,似亂非亂,亂中有序,穩中有亂。
這是一個三維空間裡的雙重繞圖,軌線看起來是在繞着兩個中心點轉圈,但又不是真正在轉圈,因為它們雖然被限制在兩翼的邊界之內,但決不與自身相交。這意味着系統的狀態永不重複,是非周期性的。也就是說, 這個具有確定係數, 確定方程, 確定初始值的系統的解, 是一個外表和整體上呈貌似規則而有序的兩翼蝴蝶形態, 而內在卻包含了無序而隨機的混沌過程的複雜結腹。當時,眼光不凡的洛倫茨準確地將此現象表述為‘確定性非周期流’。他的文章發表在1963年的《大氣科學》雜誌上。
下一篇∶蝴蝶效應 |
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 欲解中國之惑,需先鑑定中共性質(三) | |
| 2011: | 楓苑夢客:酗酒吸毒命喪黃泉 | |
| 2010: | 看看樓下老P,全伊等方舟子們的嘴臉, | |
| 2010: | 還有啊,電磁場對人體的影響。 | |
| 2009: | 基甸恩典: 謊言中的真實是喪失了力量的 | |
| 2009: | 看胡景濤的中山裝 | |
| 2008: | 看看你們這幫東西實在是中國學術界最陰 | |
| 2008: | 英語學習 精讀(36) JOURNEY WEST | |