| 天蓉:《走近混沌》-17-混沌遊戲 |
| 送交者: 天蓉 2012年11月04日14:37:07 於 [教育學術] 發送悄悄話 |
|
第十七章﹕混沌遊戲
“我想,龐加萊本質上是保守的。而且,他的數學眼光又大大超越了他的物理眼光和哲學眼光……”
李四很贊同王二的說法。對呀,你們看,他在狹義相對論的表現和他在看到混沌現象時的表現,都是出於同樣的在哲學上和物理上的保守觀念。其實,當初他已經發現了對初始條件極為敏感的混沌現象。但有人認為,龐加萊並沒有把他對同宿交錯網,也就是對混沌現象的全部想法,完全寫進他的著作。他最後提交的有關三體問題論文,有長長的270多頁,而且後來,他還就此問題,發表了三大卷《天體力學的新方法》,對天體力學做出了重要的貢獻。而對同宿交錯網及混沌,卻只是在他的書的第三卷第397節中簡單提了一下,只是為了說明:N體問題的解的複雜性,超出了人們的想象能力。
張三說:“唉,在那個時代,也難為他了……十九世紀末期,人們對自然界的基本理解是決定論的。”
的確,這種混沌的想法完全不符合當時知識界的樂觀情緒。那時的人們津津樂道的是,給定現在的狀態,人類有能力預測未來的一切!
談到這個話題,張三又想起了他們曾經討論過的決定論,上次李四不是說過嗎?根據量子力學,初始條件是無法精確確定的,這個觀點的確很有道理。張三說,儘管我不懂量子力學,但我也聽過量子力學中的不確定原理……。其實,不確定原理並不難理解嘛。在工程中,也有兩個物理量不可能同時被精確測量的情況。比如說:時間和頻率。這是因為,所謂頻率,指的是 ‘一段時間’內的振動次數。如果你把這‘一段時間’精確到一個理想的時間點的話,頻率當然就失去意義了,就像對一個時間點,速度的定義失去其意義一樣。不過,我對‘混沌現象’、‘決定’、還是‘非決定’這些概念,仍然有所疑問:
“雖然叫做混沌,看起來雜亂無章、一片混亂,雖然貌似隨機,但是,我總覺得這種混沌現象與真正的‘隨機過程’,還是風馬牛不相及,它們畢竟是確定的微分方程的解啊!另外,洛倫茨方程產生的混沌,與三體問題中的混沌,還是不同的吧?因為它們是與不同的微分方程有關嘛。所以,我們這兒討論的‘混沌’,有一些,怎麼說呢……好像仍然包含着‘決定’的成分……”
王二很快領悟到了這其中的奧妙:“難怪啊!我總看見書上把它們叫做‘決定性的混沌(deterministic chaos)’,看來這就是原因了!”
不過,王二不同意張三所說的:混沌現象與真正的隨機過程‘風馬牛不相及’這個觀點,王二提到了最近他在一本書上看到的‘混沌遊戲’。
李四也說,我們所說的‘混沌現象’,的確並不完全等同於‘隨機’。但是和隨機過程有關係,它是隨機過程和決定規律的結合。洛倫茨方程產生的混沌,顯然不同於三體問題產生的混沌,因為它們有不同形態的奇異吸引子,分別作為它們各自的標籤!這些奇異吸引子對應於不同的分形,分形有決定的一面,也有其隨機的一面。正如王二所說,從本章介紹的‘混沌遊戲’,我們將看到:分形可以從隨機過程產生出來!
總結我們迄今為止所介紹過的分形,大概有如下三類: 1. 科赫曲線、謝爾賓斯基三角形、分形龍等,可以從線性迭代過程產生; 2. 曼德勃羅集、朱利亞集,從非線性複數迭代過程產生; 3. 奇異吸引子,由洛倫茨方程或三體運動方程等非線性微分方程組產生。
前面幾章中,曾經介紹用迭代的方法構成分形。而隨機過程如何產生分形呢?我們以謝爾賓斯基三角形為例。
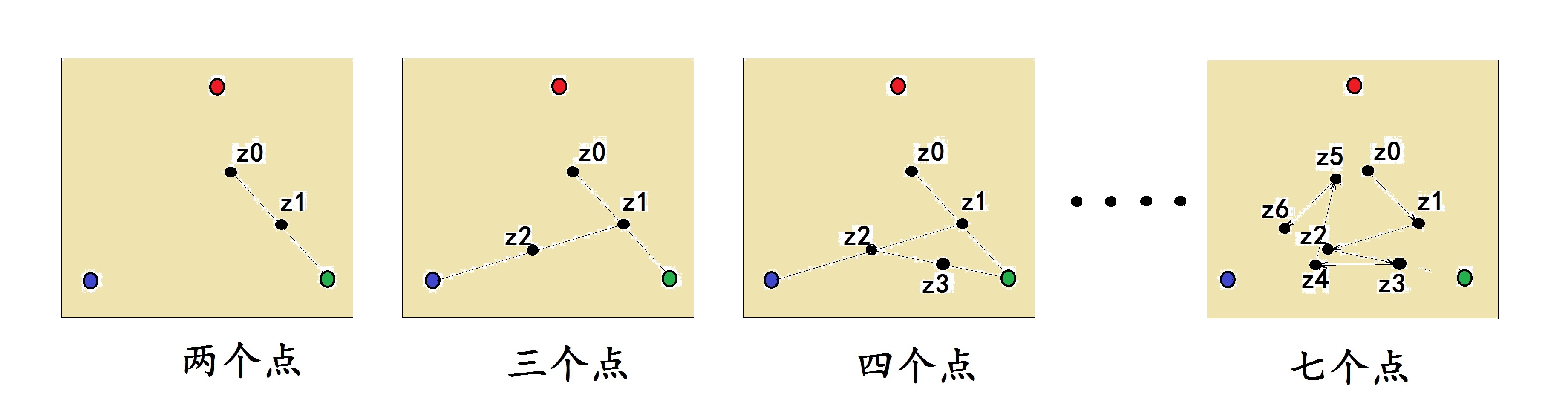
圖(17.1):用混沌遊戲方法生成謝爾賓斯基三角形
在初始圖形上,畫上紅、綠、藍三個頂點,以及隨意選擇的起始點z0,再準備一個能隨機產生‘紅、綠、藍’之一的隨機發生器。這很簡單,比如說,我們可以將標有1-6的骰子重新貼標籤:第1、4面貼‘紅’,2、5面貼‘綠’,3、6面貼‘藍’,這樣,這個骰子就能讓我們達到隨機選擇紅綠藍的目的了。然後,我們就可以開始混沌遊戲。
圖(17.1)所示,從z0開始,利用隨機選出的顏色點(這時是綠),取z0到綠點的中點,作為下一個點z1,然後,又利用再次隨機選出的顏色點(這時是藍),取z1到藍點的中點,作為z2,……以此往復地做下去,得到z3、z4、z5、z6……
張三有點不耐煩了:“你這些亂七八糟的點,看不出什麼名堂啊……”
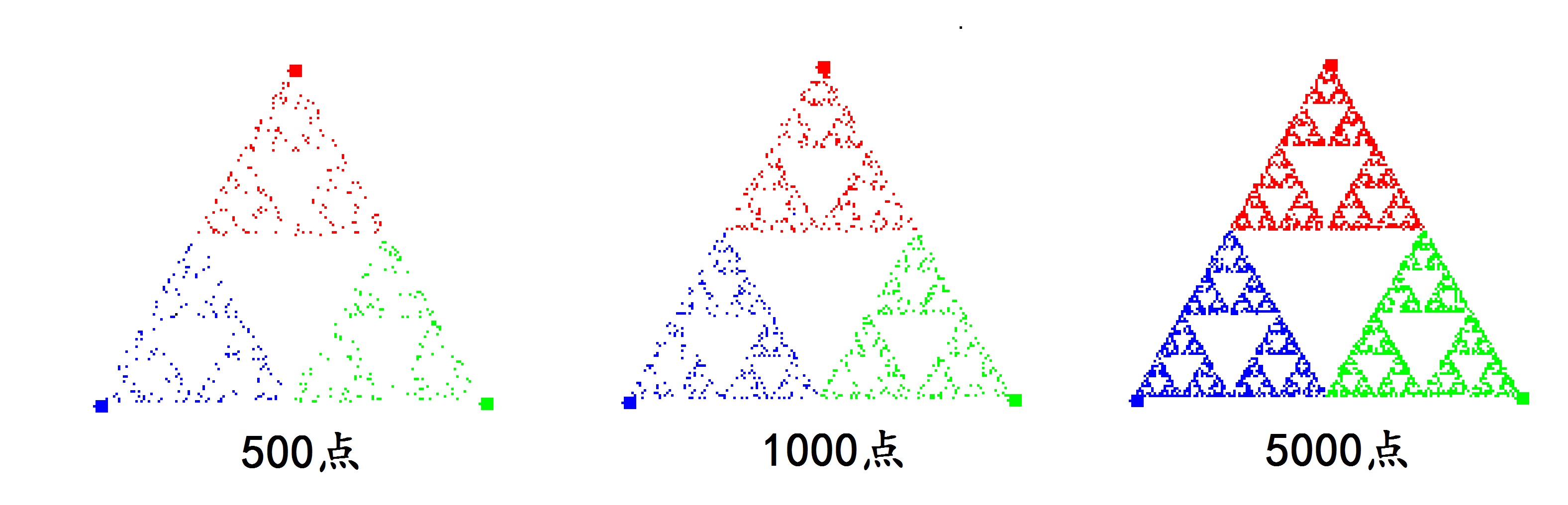
王二叫他別急,統計現象嘛,一定要足夠多的實驗點才能見效果的。果然如此,從圖(17.2)可見,如果用大量隨機的點作上面的混沌遊戲,最後構成了謝爾賓斯基三角形。
圖(17.2):生成謝爾賓斯基三角形的混沌遊戲,不同實驗點數的不同結果
張三看看圖(17.2),又回頭再去看圖(17.1),心中琢磨:像這樣,每次隨機選擇一個頂點,取中點作為下一點,一直做下去,怎麼就產生出謝爾賓斯基三角形來了呢?想着想着,腦中突然靈光一閃,似乎覺得不難理解了。因為他想起:在用迭代法產生謝爾賓斯基三角形的時候,每次迭代的過程,都是將原來圖形的尺寸縮小到二分之一,變成三個小圖形,放在三個頂點附近而成的。這迭代時的‘尺寸縮小一半’,肯定就和這兒混沌遊戲中的‘取中點’關聯起來了!不過嘛,圖形迭代時,我們看到的是同時產生了三個小三角形,像是平行運算。在混沌遊戲中,所有分形的點卻是一點接一點,串行而隨機地加到圖上去的。嘿,這就是為什麼叫做‘混沌遊戲’嘛,有意思!看起來混沌,本質上卻和迭代的效果是一樣的!
張三想通了混沌遊戲產生謝爾賓斯基三角形的奧秘,心中得意,剛想解釋給朋友們聽聽,沒料到王二已經早他幾天看過有關‘混沌遊戲’的書,比他理解得還更深一層,提出了一個他沒想過的新問題。王二問李四:
“用混沌遊戲產生謝爾賓斯基三角形比較簡單。像你說的:隨機選擇頂點,再找中點就可以了。但是,一般分形的情況怎麼辦呢?還有那些由非線性方法產生的分形呢?也能用混沌遊戲產生出來嗎?”
李四認為,原則上應該是可以的,雖然他沒有做過。數學家們的特點,不就總是從一個特殊的例子,抽象成一個一般的數學問題,再研究出一般的解決方法嗎?
產生分形所用的迭代方法,可以抽象成一組收縮變換函數,數學家們將此稱為迭代函數系統(IFS,Iterated Function System)。任何分形,只要找到了對應的IFS,就能用迭代法(或者是混沌遊戲的方法)產生出來,非線性的情況也一樣。比如說,下面公式即為謝爾賓斯基三角形的IFS:
f1(z) = z/2, f2(z) = z/2 + 1/2, f3(z) = z/2 + ( 3 + I)/2
王二點點頭,張三也覺得更明白了:啊,原來是用迭代函數系統將它們聯繫起來。謝爾賓斯基三角形的IFS中這麼多的(1/2),不就是我剛才想到的‘尺寸縮小一半’和‘取中點’此類操作的數學表達嗎?只聽王二又說:
“你剛才總結過有三類不同的分形,前面兩種分形(簡單的、和曼德勃羅集等)都顯而易見地,可從迭代過程產生。那種奇異吸引子的分形不是微分方程的解嗎?那怎麼從迭代過程產生啊?”
張三高興了,終於找到了表現的機會,趕快搶答。因為這個問題他再清楚不過了,他在畫洛倫茨吸引子等圖的時候,就是從初始時間t0時的初值開始,用迭代法產生出下一個時間t1時的值,以及再下面的t2、t3….等等時刻的數值。這樣做的原因是因為找不到微分方程的精確解,因而只能用迭代法得到數值解。
王二恍然大悟:啊,原來如此!
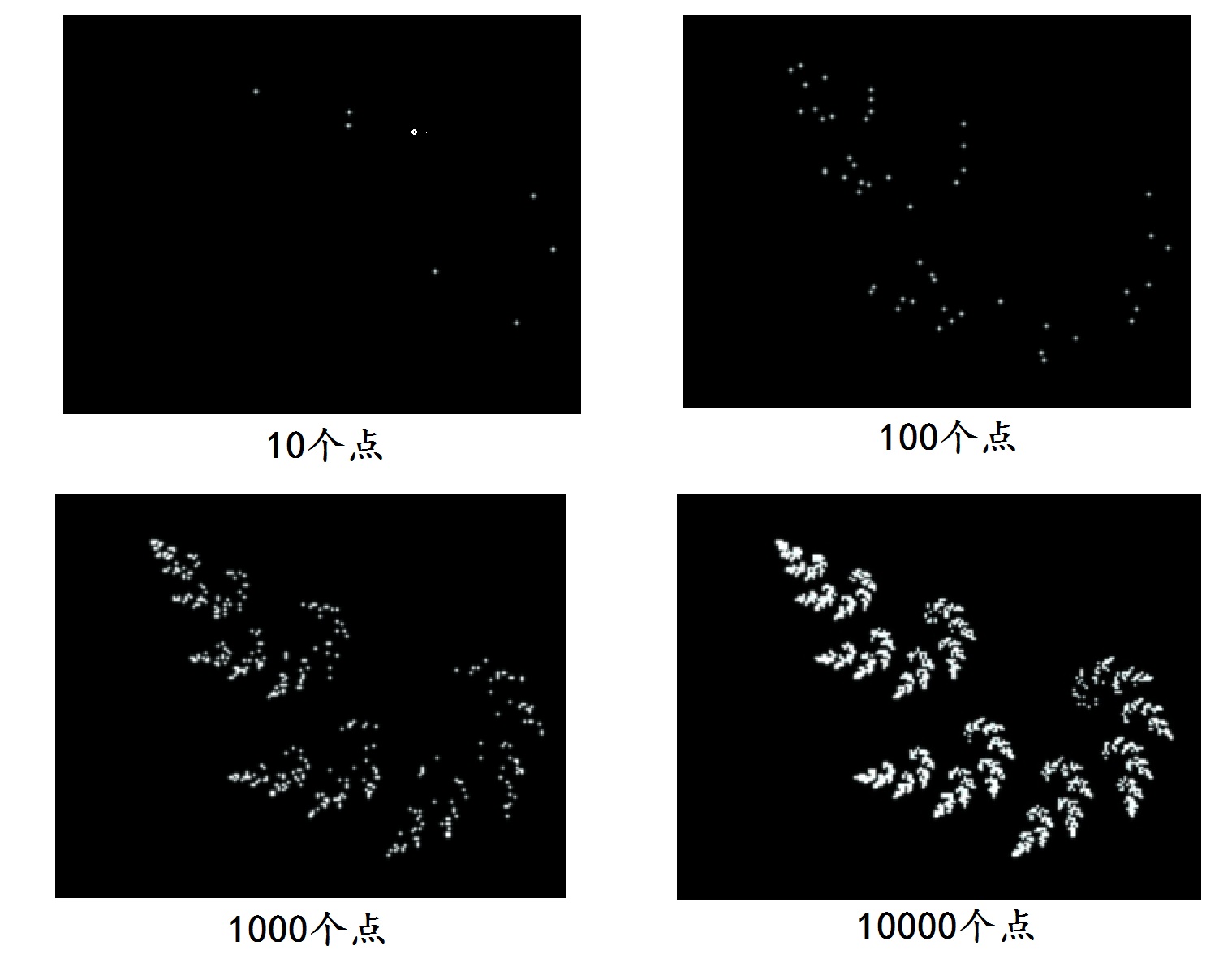
圖(17.3):生成樹葉的混沌遊戲
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 一草根:科學是什麼? | |
| 2011: | 英文詞彙學習:decimate | |
| 2010: | 大陸生活雜談:博導的精彩和大學的書店 | |
| 2010: | 思考藥渣方舟子對美國後台還有多少價值 | |
| 2009: | 為什麼國內著名的大學喜歡楊振寧而不是 | |
| 2009: | 錢學森的最後一次系統談話 | |
| 2008: | 談家楨是杜布贊斯基的“正式”PhD學生 | |
| 2008: | 我跟白字爭論的實質,不過是說他敘述史 | |