| 淺談量子計算機-2 |
| 送交者: 天蓉 2023年11月27日02:41:16 於 [教育學術] 發送悄悄話 |
3.3 量子門最簡單的量子門是量子非門,類似於經典非門,實現0、1互換,量子非門實現 |0⟩→|1⟩或|1⟩→|0⟩ ,更為一般地說,實現如下變換:a|0⟩+b|1⟩→a|1⟩+b|0⟩。
圖3.6:幾種重要單比特量子門
量子非門用矩陣X表達,被稱為X門,圖3.6中左顯示出X門的符號、矩陣表示,下面是在布洛赫球面上實現的變換。也就是說,X門是將|0⟩態矢量繞着x軸旋轉了180度,最後到達|1⟩,從而實現狀態翻轉。量子力學中有一組泡利矩陣,一組三個2×2的幺正厄米復矩陣,描述自旋和磁場之間的交互作用。其中的sX就是表示X門的X矩陣。相應地,表示Y門的Y矩陣是sY,表示Z門的Z矩陣是sZ。泡利 Y 門是一個有趣的機器,轉換得到與泡利 X 門相同的結果,|0⟩繞着y軸旋轉了180度到達|1⟩,也實現了|0⟩到|1⟩的狀態翻轉,但是是在複數的虛空間中移動的,因此,Y門實現了相位轉移和比特翻轉,泡利 Z 門使任何向量繞z軸旋轉180度,這意味着如果完全處於|0⟩、|1⟩基態,則Z 門的作用後不會發生任何變化,只有處於兩者之間的矢量才變化。
H門也叫Hadamard門,是一個非常重要的量子門。重要性是在於它的作用是使基態變成疊加態:|0⟩→a|0⟩+b|1⟩,這樣才有可能進行量子計算。其它的量子門作用在基態上,結果仍然是基態,只有H門產生疊加態。
圖3.6最右邊是 S量子門,也叫相位門。相位門保留基態|0⟩,並且將|1⟩轉換成 eiθ(乘)基態|1⟩。若 θ 等於π, 則此門化為泡利-Z門,如果旋轉π/2,則是S門,如果旋轉π/4,則是另外一種T門,圖中未畫出。因此,Z、S、T門都是特殊的相位門。
除了單比特量子門之外,還有多比特量子門,如雙比特量子門。最簡單的是CNOT,或稱“受控非門”,它的輸入是兩個量子比特,一個控制比特和一個被控比特。如果控制比特量子態為 |1⟩ ,受控比特翻轉,否則受控比特保持不變。雙比特量子門的變換矩陣是4x4的,如圖3.7中右上角CNOT門的矩陣。 圖3.7:多比特量子門 圖3.7下方的托弗利門是3量子比特門,看起來與CNOT門差不多,多了一個結點,即有兩個控制端。如果兩個控制比特是狀態 |1⟩,則對被控比特進行泡利-X運算,反之,不滿足條件則不做任何操作。托弗利門來自於一種經典通用可逆邏輯門。任意可逆電路可由托佛利門構造得到,可逆的意思是說計算過程是可逆的,邏輯電路輸入輸出交換後的結果相同。量子計算天生具有可逆性,因為量子計算每一步都是酉矩陣,酉矩陣是可逆矩陣,所以量子計算可逆。
還有一種反控(或負控)非門,如圖3.8所示。顧名思義,它的行為和(正)受控非門相反,當控制比特為|0⟩時才會翻轉受控比特。受控門也可以有多個控制比特進行組合,如圖3.8的組合控制Z門。圖3.8中黑點表示正控,空圈表示負控。
圖3.8:正控門和反控門
3.4 量子電路
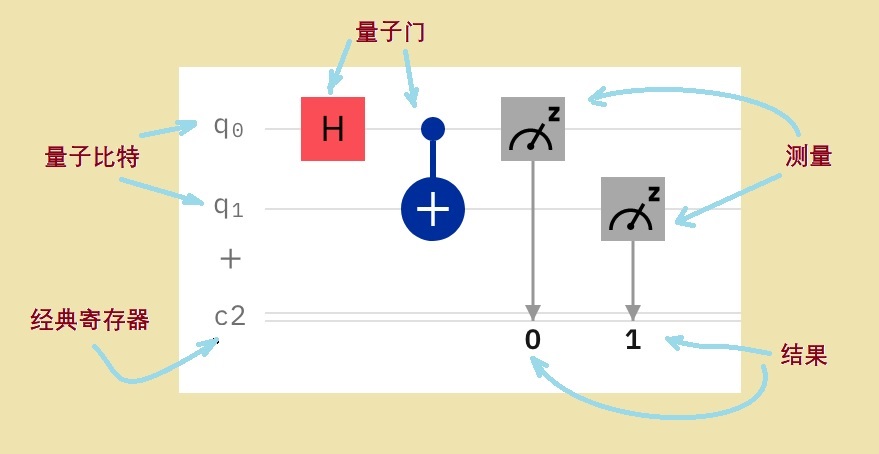
量子計算機的運算在Qubit上進行,但輸入和輸出時仍然使用經典比特,所以,整個量子計算如圖3.9中的大框圖所示,框圖中的量子計算機部分,看起來有點像經典計算機中電路圖。
圖3.9:量子電路框圖
人們用量子電路說明量子門如何控制量子信息,從而實現量子計算。量子電路是用於量子計算的模型,是執行量子位狀態的傳送之路,但它不同於傳統電路,例如:實線並不一定是物理電纜。量子電路的目的是定義事件的時間順序:水平軸是時間,左邊開始右邊結束。左邊開始的水平線是量子比特,下面的雙線代表經典比特,一般與測量相連。
類似經典電路,計算是一系列的量子門,但測量是經典電路沒有的量子操作。這些量子電路圖,都來自於IBM Quantum 模擬器【5】。
圖3.10:簡單量子電路,2個量子比特,兩個量子門,兩個測量
量子門的可逆性導致整個量子電路的可逆性,這是量子電路的特點之一。可逆性使得量子電路遵循一些特殊規則:一是只有時間順序沒有迴路(loop);二是輸入和輸出的比特數目相等(圖3.11-a)。另外,控制量子門可以完成某些簡單卻神奇的功能,例如最簡單的CNOT門,如果控制比特處於疊加態時,控制和受控比特之間就會發生量子糾纏,這是產生糾纏態的最簡單量子電路,更多的控制門能表現更多的神奇功能(圖3.11-b)。糾纏態對量子計算有什麼用呢?如對糾纏的任何一個比特施加某種操作,相當於操作施加在了所有量子比特上。
圖3.11:量子電路特例
下面舉一個簡單量子電路模擬例子,說明量子疊加態“概率幅”疊加的特別之處。
我們作如圖3.12所示的3個模擬實驗。每個實驗的上圖是電路,下方是IBM量子模擬結果。產生疊加態的操作是 H門, H門至關重要,它把基態|0⟩變成疊加態。
首先考慮實驗1,這只是一個H門作用在基態|0⟩上,從圖下方模擬結果可見:52%時間給出|0⟩,48%時間是|1⟩,就像擲一枚公平的硬幣一樣:接近 50/50概率。第二個實驗是第一個稍作改變的情形,也就是使用X門將量子位首先從|0⟩變成|1⟩,再生成另一種疊加態然後進行標準測量,結果會怎麼樣呢?
我們發現實驗結果與第一個實驗類似,除了電路不同外。結果顯示|0⟩和|1⟩的分布也接近 50/50,是53%時間給出|0⟩,47%給出|1⟩。
我們從這兩個實驗結果乍一看,感覺H門的作用類似於拋1個(公正)硬幣。
然而,H門所代表的量子隨機性,實際上與拋硬幣是完全不一樣的。讓我們再運行實驗3,就能看看有何不同。實驗3中有兩個連續的H門。如果我們認為 H門類似於拋硬幣的話,那麼兩個串聯的H門應該等於拋兩次硬幣。那麼從經典經驗,你仍然會期望接近 50/50 的分布。但是這次的結果令人驚訝,與經典不同,結果發現輸出量子位總是處於狀態|0⟩(99%的概率),似乎兩次H門的作用消除了隨機性而給出了一個確定性的結果!
圖3.12:說明量子 “概率幅”疊加的模擬實驗
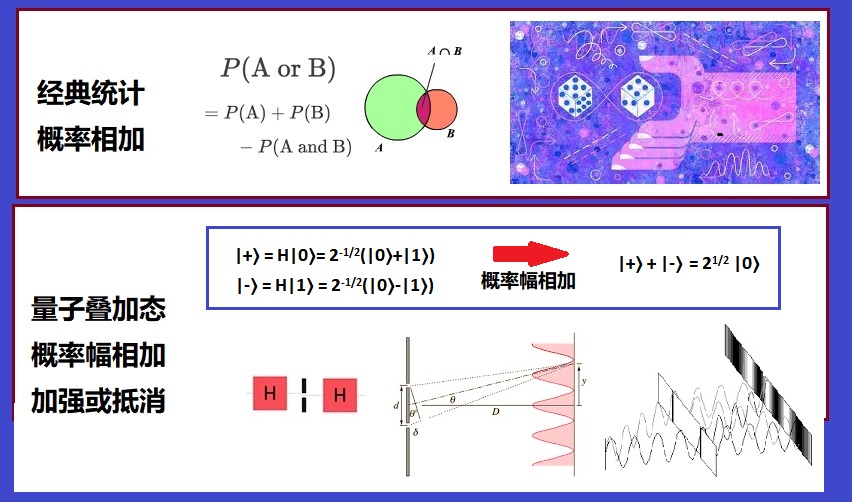
因此,量子隨機性不僅僅是經典的隨機拋硬幣。上述結果是如何產生的?在實驗1中,H門產生一個新狀態:
|+⟩ = H|0⟩= 2-1/2(|0⟩+|1⟩),
它是|0⟩和|1⟩的均勻疊加。測量使系統以相等概率處於|0⟩或|1⟩。實驗2中的新狀態是
|-⟩ = H|1⟩ = 2-1/2(|0⟩-|1⟩),
仍然是狀態|0⟩和|1⟩的均勻疊加但符號不同。實驗3可以視為兩個實驗H|0⟩和H|1⟩的總和。如果我們將這兩個實驗加在一起,狀態|1⟩會因為減號而抵消,狀態|0⟩則因加號而增強。這裡我們看到了經典概率p和量子概率幅的差異:概率幅可以是正的、負的,甚至是複數。概率幅的疊加產生干涉,而測量只能檢測經典概率無法檢測相位(負號)。
圖3.13:經典的概率相加不同於量子的概率幅相加 參考文獻:
【1】Keynote talk, 1st conference on Physics and Computation, MIT, 1981。(International Journal of Theoretical Physics, 21: 467–488, 1982) 【2】Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein; 殷建平等譯. 第1章 算法在計算機中的作用. 算法導論 原書第3版. 北京: 機械工業出版社. 2013年1月 【3】張天蓉. 世紀幽靈-走近量子糾纏(第二版)[M].合肥:中國科技大學出版社,2020年5月。 【4】Bloch Sphere(wikipedia),https://en.wikipedia.org/wiki/Bloch_sphere 【5】IBM Quantum (2022). estimator primitive (Version x.y.z) [computer software]. https://quantum-computing.ibm.com/ 相關視頻: (待續) Contents **** 1. 前言 **** **** 2. 歷史 **** **** 3. 基礎 **** 3.1 疊加態 3.2 量子比特 3.3 量子門 3.4 量子電路 **** 4. 算法 **** 4.1 Grover 量子搜索算法 4.2 多伊奇算法 4.3 秀爾算法-1(經典,數論部分) 4.4 秀爾算法-2(量子部分) **** 5. 實現 **** ********************************************************** 作者部分YouTube視頻: https://www.youtube.com/watch?v=0I8FdazqAvc&list=PL6YHSDB0mjBKB2LBZDKL9UhcMMx6GtOsx https://www.youtube.com/watch?v=_d0wquZkOYU&list=PL6YHSDB0mjBJ6qgfin-xKmP3FtTQr4x7i ********************************************************* |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2022: | 便下襄陽向洛陽 | |
| 2022: | 劉清平隨筆|人性邏輯37.“成功學”還是 | |
| 2021: | 曬枯萎的花朵-師父講故事 | |
| 2021: | 禮制主義:“殷革夏命”的打江山理念 | |
| 2020: | 儒學,最智慧的哲學 | |
| 2020: | 黃文煒:生育計劃何時休 | |
| 2019: | 社會主義研究(四) | |
| 2018: | 基因改造不能越過底線 | |
| 2018: | 王安石與凱恩斯與川普 | |