| 他的跳棋程序是人工智能的第一次展示 |
| 送交者: 天蓉 2024年05月06日08:01:36 於 [教育學術] 發送悄悄話 |
|
在1956年人工智能的第一次頭腦風暴會議上,除了來自大學及貝爾實驗室的數學家和研究人員之外,還有幾位IBM的工程師和科學家。例如:納撒尼爾·羅切斯特(Nathaniel Rochester)和亞瑟·塞謬爾(Arthur Samuel)等。羅切斯特是IBM的信息研究主管,當年達特茅斯會議發起人之一,他領導IBM的一個小組,開創了實現AI領域突破的IBM傳統;而塞繆爾,則是其小組中作出重大成果的第一位成員。塞繆爾在他獨立研發的西洋跳棋計算機程序中,首次提出並實現了如今AI的核心技術之一:“機器學習”(Machine Learning)的概念。 電腦遊戲和AI 人工智能的發展歷程中,計算機遊戲的研究一直是個亮點。特別是作為遊戲中智能之最的象棋和圍棋,被公眾喜愛,也激發科學家們的研究興趣。許多數學家和計算機學者,包括圖靈、香農、麥卡錫等,都寫過下象棋的程序。此外,許多小遊戲,諸如井字棋、五子棋、跳棋等,規則更簡單但輸贏標準明確,也需要一些細微的考慮和複雜的決策,並且很方便測試機器的計算能力及智能程度,容易將其與人類的性能進行比較。因此,就如同生物學研究中的果蠅和小白鼠一樣,遊戲成為AI研究者們的好幫手。 在棋類遊戲的計算機程序研發史上,IBM的功勞不小。這個運轉了100多年的“商業機器公司”,不愧是一個偉大的企業。它不僅數次改變了世界商業的運行模式,也在科學技術領域扮演了一個不平凡的角色。可以說,它直接促成了微軟、英特爾等新巨頭的誕生,引領了計算機科學和人工智能發展的方方面面。一百多年過去了,科學技術領域發生了翻天覆地的變化,為了應對科技的發展,IBM不斷地實驗,不停地創新,這正是它能多次轉型,將生命力延續百年而屹立不倒的秘訣之一。
圖1:參加達特茅斯AI會議的幾位IBM科學家 IBM的研究人員,開發過多種電腦遊戲軟件。從今天我們要介紹的塞繆爾的跳棋[1]開始,緊接着還有一位亞歷克斯·伯恩斯坦(Alex Bernstein),是數學家和經驗豐富的國際象棋棋手。伯恩斯坦也被邀參加了達特茅斯會議,他在會上受到麥卡錫的啟發,之後他領導幾位同事一起探索象棋程序,並最終於1957年在IBM 701上完成,這是歷史上第一個完整的國際象棋程序。再後來,IBM又有了TD-Gammon 西洋雙陸棋程序,它和塞繆爾的跳棋程序一樣,兩者都使用了讓機器通過反覆試驗來提高遊戲水平,與人類思維非常相似的學習方式,是現代機器學習技術的最早範例。 最終,在這些成就的基礎上,IBM 研究人員開發出了足夠複雜、能與人類專家競爭的神經網絡,研發了深藍(Deep Blue)的國際象棋程序,於 1997 年成為第一台擊敗國際象棋世界冠軍加里·卡斯帕羅夫的機器。 在IBM這些成果的推動下,若干公司及眾多學者的努力下,將近20年後的2016年,谷歌又進一步推出了AlphaGo,挑戰並打敗了人類的頂級圍棋大師李世石,並以4:1的比分得勝。之後,升級的阿爾法狗又以“Master”的網名約戰中日韓圍棋大師,並取得60局連勝。這些計算機弈棋的不斷進步,將機器學習、神經網絡、深度學習,蒙特卡洛搜索等多種方法集合在一起,大大推動了AI進步,最終讓它發展到今天“百花齊放”的狀態。人工智能,已經深入到了普通人的生活中。 回溯歷史,電腦遊戲的研究,伴隨着AI的進步。弈棋研究中的突破,也相應在AI歷史上豎起了一個一個的里程碑。這第一個里程碑。便是70多年前塞繆爾開發的西洋跳棋程序。 塞繆爾和電腦跳棋 亞瑟·塞謬爾(Arthur Samuel,1901—1990)生於美國堪薩斯州,他於1926年在麻省理工學院得到電機碩士的學位,然後擔任了兩年的教員後,進入貝爾實驗室從事真空管的研究,改進雷達等工作。二戰時期,他開發了一個氣體放電開關,使得一個天線能同時用於發送與接收訊息。塞謬爾於戰爭結束後,進入伊利諾伊大學香檳分校,參與開始建構ILLIAC電腦的計劃,但電腦完成前他就離開了。然後,他在1949年來到了IBM位於紐約州的實驗室。 塞謬爾最成功的成就大多是在IBM開始和進行的。他影響了IBM對晶體管計算機的早期研究,他參與了IBM 第一台存儲程序計算機 701 的開發工作。該計算機的內存基於威廉姆斯管,該管將位元存儲為陰極射線管屏幕上的帶電點。塞謬爾設法將存儲的位數從通常的 512 個增加到 2048 個,並將平均無故障時間提高到了半小時。 早在1949年,塞謬爾就有了開發跳棋程序的設想,為什麼選擇跳棋而不是國際象棋呢?因為跳棋相對簡單,但在策略上又有一定的深度,可以對人工智能和機器學習進行富有成效的研究。他於 1952 年首次為 IBM 701 編寫跳棋程序,並且於 1955 年完成了具有良好棋藝技巧的第一個程序。
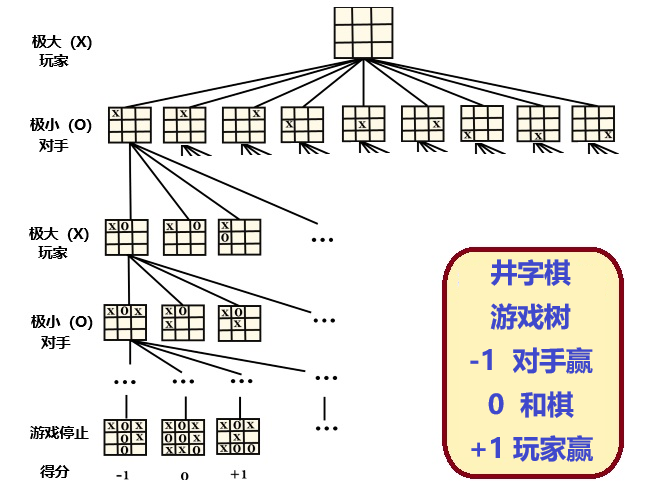
圖2:電視節目中,塞繆爾在IBM 701上向公眾展示計算機“跳棋” 1956年2月24日,塞繆爾的“跳棋”節目在IBM 701上運行,在電視上向公眾展示和播放。這程式因為表明了當年電腦硬件的進步和作者的程式編寫技巧而轟動一時。當該程序即將演示之前,IBM 創始人兼總裁老沃森高興地預測,這個電視播放將使 IBM 股票價格上漲 15 點!之後的效果果然印證了沃森這句話。除此之外的另一個收穫是,這個電視節目使公眾第一次認識到,電腦不僅可以用作複雜的數學計算,也能用於帶娛樂性質的遊戲。這被公認為是人工智能的首次展示,這個程序也被認為能夠“學習”,讓人們首次了解到:計算機的確可以具有“智能”! 塞繆爾的“跳棋”節目電視播放幾個月後,正值達特茅斯研討會召開,多位與會者都熱衷於研究計算機弈棋技巧,成為討論的熱門話題。 1966年,塞謬爾自IBM退休並成為斯坦福大學教授,之後他在斯坦福擔任教職直至1990年因帕金森氏症併發症而去世。在斯坦福時他繼續研究西洋跳棋,直到70 年代時他的跳棋程序被更先進的方法所替代。他也與著名的計算機專家高德納發展TeX計劃,並為之撰寫了文件,據說他在88歲生日後依舊撰寫程式。 塞謬爾是一位謙虛低調、埋頭苦幹的學者,客觀務實且樂於助人,特別是在他了解並擅長的許多領域,盡其所能地幫助其他人。 下面,我們簡要解釋一下塞謬爾在跳棋程序中採用的Minimax算法,以及如何讓機器自我學習,真實地體會一下AI中的電腦弈棋是如何工作的。 極小極大(Minimax)算法 塞謬爾思考,如何設計一個複雜的程序來下跳棋?他記起香農曾經寫過關於用機器下國際象棋的文章[2],猜想香農知道如何構建程序。1949 年,當塞繆爾前往芝加哥去見香農時,才知道具體程序實際上還沒有被創建出來,香農只是籠統地泛泛而談,並沒有真正涉及到計算機。因此,塞謬爾決定動手編寫一個能夠展現這一普遍問題的機器下棋智能程序,因為它可以提供解決此類戰略問題的一般結構。 香農提出的基礎算法今天被稱為Minimax(極小極大算法),以馮·諾伊曼提出並證明了的極小極大值定理命名。這個方法適合於兩個玩家對弈的遊戲。為了方便解釋,我們且將他們稱為“玩家”和“對手”。“極小極大”的意思是說,遊戲玩家應該如此行動,以儘量“減小”(極小化)可能的最壞情形下的“最大”損失。這兒所說的“極小“和”極大“,都是針對玩家而言的,而“對手”的策略,則與玩家的策略相反。 說得更為具體一點,假設玩家和 “對手”都會考慮整個遊戲的未來狀態,那麼,你的每一步應該這樣選擇:即使對手也總能按照同樣策略來選擇他的最佳回應,但在比賽結束時你仍然可以獲得你能得到的最好結果,或者說,將最大風險極小化。 計算機的原理是數值計算,因此,剛才敘述的“極小極大”思想需要量化。因為弈棋過程實際上就是棋盤上棋子分布狀態一步一步改變的過程,所以,量化可以通過一個“狀態S的價值函數F(S)”來達到。狀態函數F(S)賦予每個狀態一個數值,來評估不同狀態對玩家的優劣,函數值大利於玩家。所以,在下面例子中說法反過來了:玩家的目標是最大化max獲勝位置的價值,對手則要減小min狀態函數值。 對計算機程序而言,遊戲開始之前,起碼需要做到兩點:一是根據遊戲規則,產生一個遊戲的“路徑樹“,即根據遊戲規則,從當前狀態生成所有可能的下一個狀態,以及這些狀態的再下一個可能狀態,等等。二是定義對玩家(這兒是計算機)有利的價值函數,即給路徑樹上每個狀態賦值。 例如,考慮一個非常簡單的“井字棋“遊戲,規則是兩方輪流、一次一步,首先將3個棋子連成一線(橫豎斜)的一方為贏家。圖3是簡化了的井字棋的遊戲路徑樹及狀態函數值。 從圖中可見,玩家(X)先走第一步,這時有9種可能的選擇;對手第二步,8種選擇;然後遊戲繼續直到結束。結束時的狀態函數值(+1、0、-1)決定最後的輸贏。
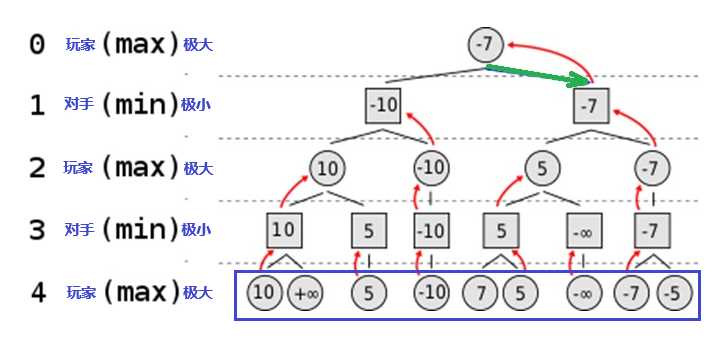
圖3:井字棋的部分路徑樹和最後得分 按照剛才的說法,玩家得分越高贏的可能性越大,反之,“對手“分低為贏。因此,玩家根據評分函數走分數最高的棋步。機器的程序一旦確定了,便只按照最佳路徑的動作來達到最佳遊戲結局,並不在乎對手可能犯下的錯誤。 為了說明極小極大算法之原理,上述井字棋仍然太複雜,因此再舉下面更簡單的例子,見圖4。 假設正在玩的遊戲每步每一方最多只有兩種可能的動作。該算法生成了圖4的路徑樹,這兒只有4步遊戲過程。你不用糾結於“這是什麼遊戲,遊戲的規則如何,何種狀態函數”等等問題,但我們知道它有如圖所示的路徑樹,以及最下一排的狀態,即最後一排藍框裡的圓圈中顯示的數值。 當狀態函數等於正無窮大“+∞”,玩家贏;函數等於負無窮大“-∞”,對手贏;因此玩家總是選擇狀態函數值最大,即max的路徑;對手總是選擇狀態評價函數值最小,即min的路徑。
圖4:極小極大法一例 根據上述原則,可以從路徑樹,以及最下一排的數值,倒推回去來決定玩家的第一步應該怎麼走,才符合Minimax算法的要求,圖4中,倒回去的步法用紅箭頭表示。 根據Minimax算法的原則,對該例所示的情形得到的結論是:玩家的第一步應該選擇往右走一步,也就是圖中綠色箭頭所指的位置。這樣選擇後,每一步沿着紅箭頭的反方向朝下走,第四步得到的評價函數值等於-7。儘管不是“+∞”,但已經是該特定情況下玩家可能取得的最好結果。 機器學習 上面說到的狀態評價函數F(S)很重要,它決定了計算機的下棋能力。如果用人來打比方的話,就好比是每一個奕棋者腦袋裡都有一個他自己的F(S),從這個函數,他與人對弈時可以看到好幾步後的情形,從而來選擇當下更“好”的一步。 看到這兒,你可能會說:那好啊,讓計算機模擬國際冠軍腦袋中的評價函數不就行了嗎?或者你會認為,下棋高手可以建造出更高明的走棋程序。 其實不然,產生上述想法的根源是因為忽視了“學習”。 人類具有學習的能力,這是顯示智力的重要標誌之一。那麼,能否使機器也具有這種能力呢?為了達到這樣的目的,塞繆爾引入了一種機制,讓他的跳棋程序可以從已經玩過的遊戲中學習。塞繆爾讓計算機記錄了它看到的每個位置以及該位置最終是否導致勝利或失敗;將這些經驗納入其後續決策中,程序玩的遊戲越多,效果就越好。塞繆爾將這一過程稱為“機器學習”,他創造的這個術語至今仍然是人工智能的核心。1962 年,塞繆爾跳棋在與自己進行了數千場對弈以提高其技能後,擊敗了自稱“跳棋大師”的羅伯特·尼利。隨後,儘管它與人類對手的戰績參差不齊,但塞繆爾制定的原則為 20 世紀 90 年代 IBM 在人工智能方面的一系列突破奠定了基礎。 人類下棋高手也是從下棋的經驗中“學習”才取得成功的,機器的優勢是在於它的速度和精確性,假設人類棋手一年下1,000 盤棋,而計算機幾天或幾小時就可以達到這個目標。因此,計算機的速度使它有可能在短期內被訓練而達到專業棋手級的水平。 塞繆爾跳棋的關鍵之處就是在於它能“學習”,在它訓練和學習的階段,它可以不斷地更新它的評價函數F(S)。塞繆爾為他的跳棋設計的學習方法,叫做“時間差分學習”方法。從今天機器學習的分類來看,是屬於強化學習[3]。 現代機器學習大體分為3類:監督學習、無監督學習、強化學習,見圖5。 監督學習是從有標記的訓練數據中推導出預測函數,即給定數據,預測新數據。例子:孩子學認字,預測公司收益等。 無監督學習是從無標記的訓練數據中推斷結論,即在給定數據的引導下,尋找隱藏的結構。例子:孩子通過自己每天觀察到的各種事物,自動將其分類和識別:動物、植物、鳥、房屋等等。 強化學習關注的是與環境的互動:採取行動,從環境得到反饋,然後逐步改進行動的策略。例子:學習下棋的過程。
圖5:機器學習種類 跳棋程序在下棋的過程中,棋手走的每一步棋存在“好壞”之分,如果下得好,是一步好棋;下得不好,則是一步臭棋。評價函數給每一步行動後的狀態賦值,相當於環境給出了一個明確的反饋,是好還是壞?“好壞”程度如何?然後,機器再根據反饋來更新它的評價函數。 塞繆爾的跳棋程序採用時間差分技術,通過自身的行動和獎勵來進行學習。時間差分學習的關鍵見解是即使沒有關於最終結果的知識,狀態的價值可以根據後續狀態的價值來進行更新。 培訓過程中,該程序會從隨機位置開始自我對戰多局。每一步,程序都會選擇能夠最大化獲勝機會的移動,根據當前狀態價值函數進行決策。隨着遊戲的進行,該程序會使用一個公式來更新狀態價值函數,該公式將當前狀態的價值估計和下一個狀態的價值估計結合起來。這個更新被稱為時間差分,因為它測量了當前狀態的價值估計和下一個狀態的價值估計之間的差異。通過反覆進行這個過程,並不斷更新狀態價值函數。通過反覆進行這個過程,並不斷更新狀態價值函數,程序逐漸改善了其下棋能力。 塞繆爾的時間差分學習為強化學習領域帶來了重要的突破,它的應用廣泛,包括機器人技術、決策系統等各個領域。 塞繆爾的工作對現代機器學習產生了深遠的影響。他的國際跳棋程序展示了機器能夠通過迭代反饋和經驗來學習並提高性能的潛力。他在自主學習、強化學習、特徵提取和泛化等方面的貢獻,影響了後續機器學習算法的發展。塞繆爾的研究激發了人們對機器學習的熱情和探索,推動了神經網絡、決策樹、強化學習和其他機器學習技術的進步。 塞繆爾1952年首次開發的跳棋程序,被廣泛認為是人工智能和機器學習領域的一項重大成就。 參考文獻: [1]維基百科(Arthur Samuel) https://en.wikipedia.org/wiki/Arthur_Samuel_(computer_scientist) [2]Claude Shannon (1950). "Programming a Computer for Playing Chess" (PDF). Philosophical Magazine. 41 (314). [3]Samuel, A. L. (1959). Some studies in machine learning using the game of checkers. IBM Journal of research and development, 3(3), 210-229. (本文首發於微信公眾號“知識分子”) |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2023: | 搞情報:六四後麋國總桶老不死給中國人 | |
| 2023: | 畢業與櫻花時節 | |
| 2022: | 戰略分析(17):俄國侵烏將以俄撤兵陪款 | |
| 2022: | 前世今生論 | |
| 2021: | 愛欲與活力之於四角作用和四環作用 | |
| 2021: | 漢儒搞和平演變的成功 | |
| 2020: | 玉帝遣神 等(二則) | |
| 2020: | 數據庫安全能力:安全威脅TOp5 | |
| 2019: | 陳獨秀們反儒反華的鐵證 | |
| 2019: | 無淘汰制的鋼琴比賽 | |