| 【數學】實用的拉丁方 |
| 送交者: gugeren 2017年05月25日09:53:17 於 [教育學術] 發送悄悄話 |
|
【數學】實用的拉丁方 提起拉丁方(Latin square),做過藥物實驗設計的網友應該對它不陌生。 拉丁方(陣)是一種 n × n 的方陣。在這種 n × n 的方陣里,擁有 n 種不同的元素,每一種不同的元素在同一行或同一列里僅出現1次。 【圖1:拉丁方】
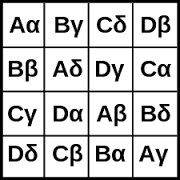
實際上,人們在實際生活中使用的,是拉丁方的一種特殊形式,稱“正交拉丁方(orthogonal Latin square)”。 正交拉丁方,學名是“希臘拉丁方(Graeco Latin square)”。這樣的拉丁方內,至少由2個不同的字符、顏色或字體等組合成為方陣內的每個元素,而且沒有同樣的元素組合會出現在同一個拉丁方內。 【圖2:正交拉丁方】
正交拉丁方可用於科學實驗的設計和體育賽程的編排。 歐拉在研究了拉丁方以及正交拉丁方以後,他證明了: 1】不存在2-階正交拉丁方。 2】當n為奇數,或n為4的倍數時,存在正交n-階拉丁方。 3】剩下則是2倍奇數階的正交拉丁方:6, 10, 14, 18, ...。 可以看出,歐拉解決了所有自然數階的正交拉丁方的四分之三的內容。 由於歐拉費盡心機製作不出6階的正交拉丁方,他推測不存在6階的正交拉丁方,從而又引申出不存在所有的3】的情況。 但是,這次歐拉的猜測是錯誤的。 1901年,法國數學家Gaston Tarry(1843-1931)證明了6階正交拉丁方不存在。 1960年,3位美國數學家Ernest Tilden Parker(1926-1991),Raj Chandra Bose(1901-1987)和Sharadchandra Shankar Shrikhande(1917-)證明了存在除了6階以外的所有2倍奇數階的正交拉丁方。 更加複雜的正交拉丁方還有: 相互正交拉丁方(Mutually orthogonal Latin squares) 【圖3:Mutually orthogonal Latin squares】
== 相關鏈接: 拉丁方: https://en.wikipedia.org/wiki/Latin_square 正交(希臘)拉丁方: https://en.wikipedia.org/wiki/Graeco-Latin_square 相互正交拉丁方: https://en.wikipedia.org/wiki/Graeco-Latin_square#Mutually_orthogonal_Latin_squares |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2016: | 中國通:習近平似蔣介石(命運也將一樣 | |
| 2016: | 推背圖第四四象所說的聖人就是在芬蘭的 | |
| 2015: | 範例世界-從“經驗與知識同一”說起(C) | |
| 2015: | 一位小學生天天看《新聞聯播》,竟然寫 | |
| 2014: | 美國小孩為什麼學不好英文 | |
| 2013: | c_y_lo, 請教個英語問題 | |
| 2013: | 範例哲學如何解決笛卡爾的“心靈-身體 | |
| 2012: | 親子相認是基本的人性 | |
| 2012: | 馬寅初有兩妻七孩,是個口是心非的不良 | |