| 數字也有危機?(第一次數學危機) |
| 送交者: 天蓉 2021年12月29日06:59:53 於 [教育學術] 發送悄悄話 |
|
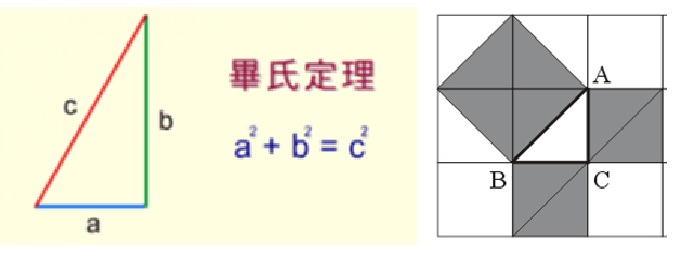
大家都知道,一個國家或地區的經濟會發生“經濟危機”,沒想到數學這種象牙塔中的理論研究也會發生危機。歷史上的數學危機有三次,本文介紹第一次。 第一次數學危機發生於古希臘時代。古希臘的泰勒斯(Thales,公元前624年-公元前546年)被學界譽為第一位數學家,他第一次將“證明”的思想引入,為數學注入理性精神。古希臘的思想家們追溯萬物之源,思想活躍、不落俗套、敢於出新。各種靈巧怪異的想法紛紛湧現出來,聽起來令人感覺妙趣橫生。如泰勒斯認為“萬物皆水”,他的一位學生主張“萬物皆氣”,另一位學生認為萬物起源於某種虛無縹緲不定形的東西…… 1,畢達哥拉斯其人 離泰勒斯活躍的米利都不遠處,有一個叫薩摩斯島的城邦,則出了一位主張“萬物皆數”的數學家,認為“數”可以解釋世界上的一切事物。這是畢達哥拉斯(Pythagoras,前570年-前495年),他既是數學家,也是哲學家和音樂理論家。他對數字痴迷到近乎崇拜;同時認為一切真理都可以用比例、平方及直角三角形去反映和證實。他的畢達哥拉斯學派除了將數學推崇到極致之外,還具有一些不可思議的神秘主義因素。例如,他們認為吃蠶豆是不道德的,因為人死之後,靈魂會寄存在蠶豆中,據說畢達哥拉斯本人可以與牲畜交談,以便告訴牲畜不要吃蠶豆。 圖1:畢達哥拉斯(點擊觀視頻) 畢達哥拉斯與泰勒斯相差50多年,曾經見過泰勒斯並受他以及米利都學派的影響,可以算是泰勒斯的學生。畢達哥拉斯曾用數學研究樂律,首次發現了音調的音程按弦長比例產生,頻率間隔比例的簡單數值形成了美妙和諧的聲音。由此,畢達哥拉斯將自己有關數的理論結合米利都學派的宇宙論,提出了宇宙無比“和諧”的概念。他用數學關係表達音調的特質,他認為這些關係也呈現在視覺、角度、形狀中……所有的比例都是按照完美的數字構成的!太陽、月亮和行星都散發着自己獨特的嗡嗡聲(軌道共振) ,地球上生命的特性反映了人耳察覺不到的這些天體的聲音。 畢達哥拉斯第一次提出了大地是球體這一概念,從他開始,希臘哲學產生了數學的傳統,對以後古希臘的哲學家有重大影響。 2,畢氏學派對數學的貢獻 畢氏學派證明了畢達哥拉斯定理(勾股定理),這和其他很多文明中發現許多勾股數的意義是不同的。勾股數是符合勾股定理的三元數組,它們的數目有無窮多。例如,(3,4,5), (5,12,13), (8,15,17), (7,24,25)…等等,都是勾股數,中國古代的“勾三股四弦五”就是典型的例子。在公元前18世紀的巴比倫石板上,就已經記錄了各種勾股數組,最大的是(18541,12709,13500)。發現了勾股數,不等於發現了勾股定理,更不等於證明了勾股定理。這個定理的證明,是始於畢達哥拉斯,再由後來的歐幾里得給出了清晰完整的證明。
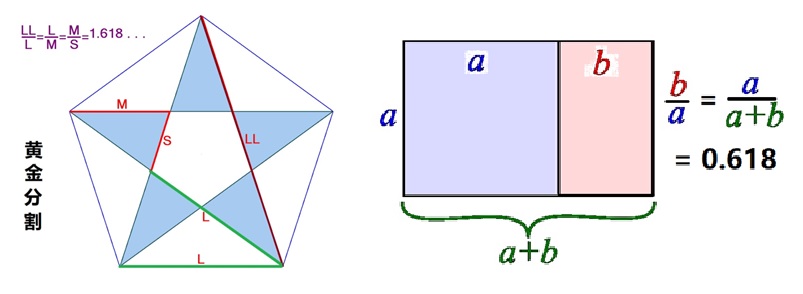
圖2:畢達哥拉斯定理 畢達哥拉斯學派還研究過正五邊形和正十邊形的作圖,得到黃金分割的比值數:(1:0.618)。
圖3:黃金分割 除了諸如證明勾股定理這種具體的貢獻之外,畢氏學派當時最著名的數學思想是用原子論的觀點,將幾何建於算術(整數)之上。根據畢達哥拉斯學派的觀點,一切數都可以用整數以及整數的比值(即我們現在所說的“有理數”)表示出來。 當年的古希臘,各種哲學思想派別林立、此消彼長。畢達哥拉斯欣賞原子論的觀點,並把它用於數學,用原子觀點來構建他的幾何綱領。 原子論認為萬物分下去是原子,而畢氏學派認為幾何線段分下去是“點”。點是什麼呢?就是幾何的原子,和原子一樣有大小,即其長度不為零 。例如,設d表示點的長度,d有三種可能性:d = 0, d = 無窮小,d>0。
圖4:畢氏學派用原子論觀點解釋幾何線段 對“點”的理解反映了當時數學界連續派和離散派觀點的區別,根據連續派的說法,線段無限可分,最後的“點”無尺寸,大小為零,或有人說是“無窮小”。但畢氏學派認為:如果說點是0,那麼,無尺寸的“點”,如何能構成有尺寸的線段呢?這是無中生有、自相矛盾的。如果說點是無窮小,那麼無窮小是什麼?也說不清楚,令人困惑,更顯得詭秘深奧。因此,畢氏學派採取離散派的觀點,認為“分割”有盡頭,最後的“點”很小但不為零。換言之,在畢氏學派看來,線段就像是許多珠子串在一起的珍珠項鍊。基於畢氏的幾何觀,任何兩個線段都可以共度(或稱公度、通約),因為它們都由某個最小的長度組成。也就是說,所有的數都可以表示為整數或者整數之比。因此,世界及宇宙的美妙與和諧就建立在整數的基礎之上! 3,希帕索斯發現無理數
圖5:發現無理數的希帕索斯(點擊觀視頻) 誰知好景不長,畢達哥拉斯的一位學生希帕索斯發現了√2這種無法用整數或整數之比來表示的數(之後被稱為“無理數”)。 事實上,從畢氏學派證明了的勾股定理,是很容易發現無理數的。一個邊長為1的正方形,其對角線便不能與邊長通約,長度記為√2。類似情形還有很多很多:面積等於3、5、6、……17的正方形的邊,與單位正方形的邊也都不可通約。無理數的存在逐漸成為並不罕見人所共知的事實。√2與1不可通約,可以用如下反證法證明:
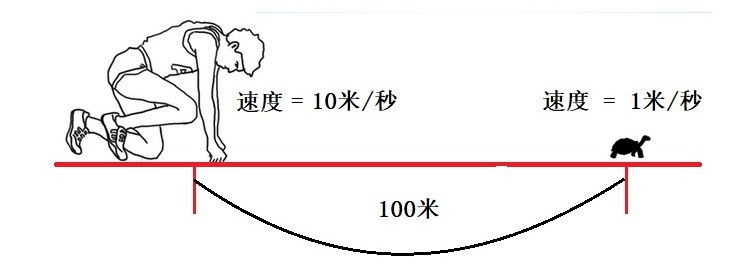
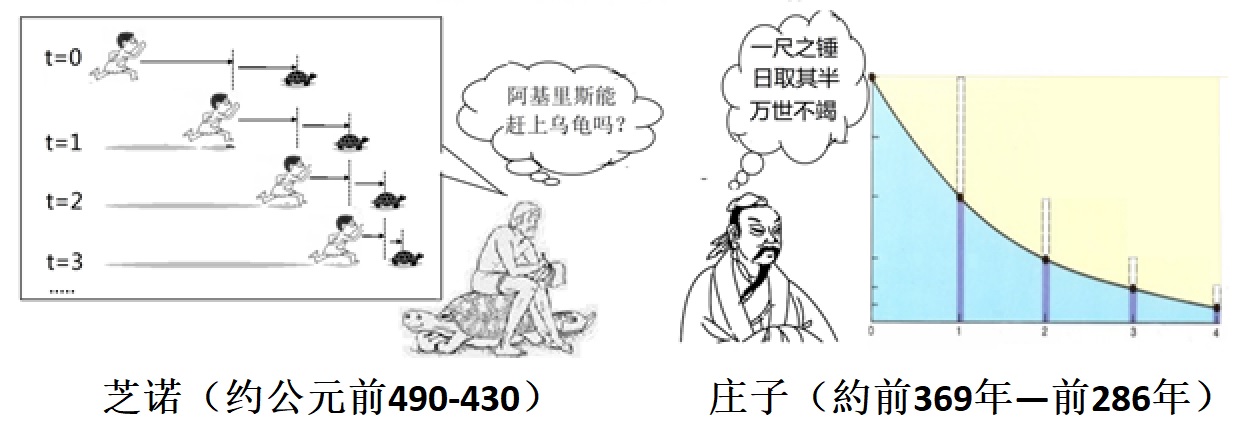
無理數的發現,對於依靠整數的畢氏哲學,是一次致命的打擊。因此,據說當時他們將這些事實嚴格保密,緘口不言,不想被不識時務的希帕索斯給捅了出來!唉,別無他法,只有將他丟到海中餵魚,才能解除一點同窗學子們的心頭怨恨。 不過是發現了一種不能通約的數而已,有這麼嚴重嗎?情況的確挺嚴重的,因為:如果存在不可通約的線段,就沒有公共的量度單位,便不能將“點”看成有長度的東西,畢氏學派“萬物皆(整)數”的哲學思想立刻分崩離析,建立於美妙的整數之上的和諧宇宙也轟然倒塌了!畢氏學派證明的幾何命題、他們關於相似形的一般理論,都局限在可通約的量上。人們自然便懷疑:數學作為一門精確的科學是否還有可能?宇宙的和諧性是否還存在? 因此,無理數的發現,引起了第一次數學危機。 4,芝諾悖論衝擊極限概念 沒過多久,生活在另一個古希臘城邦埃利亞的芝諾(Zeno of Elea,公元前490-430),又提出了幾個怪怪的、似乎扯不清楚的“悖論”,更加深了人們的危機感,以及對美好和諧世界的擔憂。 芝諾是著名哲學家巴門尼德的學生,因提出四個有關運動的悖論而知名。其中的阿基里斯悖論與數學中極限理論密切相關,在此重點介紹一下。 阿基里斯是古希臘神話的善跑英雄,希臘第一勇士,假設他跑步的速度為烏龜的十倍:例如,阿基里斯10米/秒,烏龜1米/秒。出發時,烏龜在前面100米處,如圖7所示。
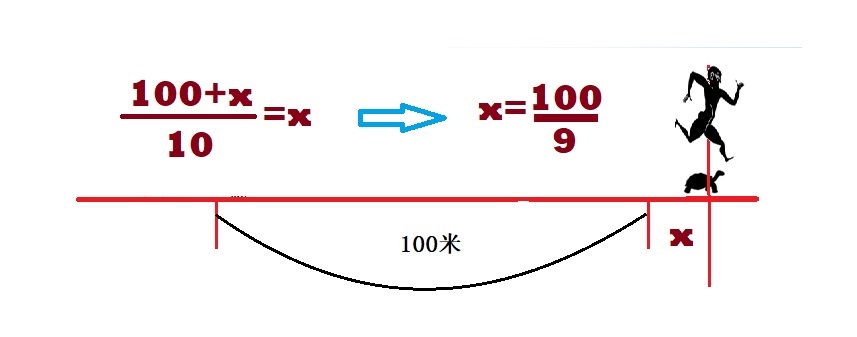
圖7:阿基里斯追烏龜 按照常識,阿基里斯很快就能追上並超過烏龜。 芝諾卻說:“他永遠都趕不上烏龜!” 為什麼?芝諾振振有詞:開始,烏龜超前100米;當他跑了100米到烏龜開始位置時,烏龜已經向前爬了10米,烏龜超前10米。然後下一步,烏龜將超前1米;再下一步,超前0.1米;然後繼續下去:超前0.01米、0.001米、0.0001米……不管這個數值變得多麼小,烏龜永遠超前! 用我們現代的數學知識,一個簡單的代數計算就足以反駁芝諾的“謬論”。 假設某個時刻x秒之後,阿基里斯追上了烏龜(圖8),可以列出x滿足的方程並解出x=(100/9)。也就是說,11又1/9秒之後,阿基里斯趕上了烏龜! 因此,現在的大多數人會覺得芝諾是在“詭辯”,因為他說的烏龜超前的一連串數字:1米、0.1米、0.01米、0.001米、……,貌似無窮多,但都是在(100/9)秒之內完成的,並非“永遠”! 當我們說到“無限”, 有兩種含義: 一是無限分割, 一是無限延伸。無限份時間不等於無限長時間!一個收斂級數的和是有限的。而時間的流逝卻是無限的。芝諾顯然混淆了兩者,或者偷換了概念。因此,以現代觀點看,他的確是在“狡辯”。 不過,我們需要用歷史的眼光分析這個問題。那是兩千多年前,還沒有完善的極限概念,可能也不知道“收斂級數”這個詞,而這正是我們得到上面結論的基礎。比芝諾稍後(200年左右)的阿基米德(前287年-前212年)對此悖論進行了頗為詳細的研究。他把每次追趕的路程相加起來計算阿基里斯和烏龜到底跑了多遠,將這問題歸結為無窮級數求和的問題,證明了儘管路程可以無限分割,但整個追趕過程是在一個有限的長度中。所以說,芝諾的說法並非僅僅是狡辯。 5,芝諾悖論的意義
圖9:極限思想的萌芽 “一尺之棰,日取其半,萬世不竭”,這句話是中國惠施(前370年-前310年)說的。意思是說,一尺長的竿,每天截取一半,一萬年也截不完。竿子越來越短,長度越來越趨於零,但又永遠不會等於零,這正是“事物無限可分,但又不可窮盡”的極限思想的萌芽。
圖10:不同的極限觀點 前面說到的畢氏學派用原子論解釋幾何的數學觀,代表了古希臘極限觀。
芝諾時代已經過去二千四百多年了,但是圍繞芝諾的爭論還沒有休止。芝諾揭示了稠密性連續性、無限可分和有限長度、連續和離散、實無窮潛無窮之間的關係。引起人們對這些關係的關注與研究。
圖11:實無窮和潛無窮 實無窮把極限當作數學實體,潛無窮認為極限是無限趨近的過程。古時候,畢氏學派代表 “實無窮”的極限觀,惠施的說法是“潛無窮”觀點。 因此,在希臘數學發展的關鍵時刻,芝諾也做出了有意義的貢獻。 6,第一次數學危機的解決 第一次數學危機被柏拉圖(Plato,公元前429年-前347年)的弟子歐多克索斯(Eudoxus of Cnidus,公元前408年-前355年)創立了新的比例論、完善了窮竭法而克服。 歐多克索斯也屬於畢氏學派,是畢達哥拉斯弟子阿爾庫塔斯(Archytas,前428年-前347年)的學生。因此,第一次數學危機的解決可說是“解鈴還需系鈴人”。也可以說,無理數的發現,當年是畢氏學派的最大災難,其實也是畢氏學派的最大成就。 歐多克索斯處理不可通約量的方法,出現在歐幾里得(前325年-前265年)《幾何原本》第5卷中,和狄德金於1872年繪出的無理數的現代解釋基本一致。他給出的比例的定義與所涉及的量是否有公度無關,這樣就容許了無理數的存在。 第一次數學危機使整數的尊祟地位受到挑戰,使古希臘的數學基礎發生了根本性的變化。在第一次數學危機之前,古希臘的數學是以數為基礎的。第一次數學危機之後,古希臘的數學基礎則轉向幾何,以幾何為基礎,幾何學開始在希臘數學中占具特殊地位使,數學的公理化成為可能。危機的解決也推動了數學及其相關學科的發展。 同時,第一次數學危機也表明了直覺和經驗不一定可靠,推理證明才是可信的。從此希臘人開始建立幾何學公理體系,直到後來的歐幾里得。因此,公理化思想是數學思想上的一次革命,是第一次數學危機的自然產物。 由此產生的歐幾里得幾何對數理天文學的發展有重大意義。由於宇宙是幾何的,宇宙的規律是幾何規律,因此研究宇宙就離不開幾何圖形以及幾何理論。 回顧一下歷史事實便知,數學基礎從整數轉向幾何意義頗大。古代以數為基礎的文明,很難建立數學的公理系統。古代中國和古印度古埃及都是例子。在這些國家從未建立起數學的公理系統。 因此,第一次數學危機,是整個科學發展進程中的一個重要事件,對科學的發展起了促進作用。 ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× 本人的科普視頻:YouTube: 天文航天:“談天說地” https://www.youtube.com/playlist?list=PL6YHSDB0mjBLmFkh2_9b9fAlN7C4618gK 趣味數學:數學大觀園 https://www.youtube.com/playlist?list=PL6YHSDB0mjBJifi3hkHL25P3K9T-bmzeA 也發在微信公眾號“天舸”上(微信號:gh_e01fc368fe31):
長按/掃一掃二維碼,敬請關注我的微信公眾號“天舸” ! ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× |
|
 | |
|
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2020: | 《鋼鐵是怎樣煉成的》的兩個版本 | |
| 2020: | 美中教育雲泥之別.六 | |
| 2019: | 楊醫生被某殺與人均預期壽命的毛澤東階 | |
| 2018: | 佛道兩家之爭 眾神會維護哪一邊? | |
| 2018: | 580、,一句真話比整個世界的分量還重 | |
| 2017: | 《芳華》的“好人”為啥沒好報? | |
| 2017: | 彭運生談藝錄(154) | |
| 2016: | 作為戰略學者,戰略是頭等的,學問次之 | |
| 2016: | 在努力中,又觀見一些嚴重的事 | |