| 天蓉:《走近混沌》-22-再回魔鬼聚合物 |
| 送交者: 天蓉 2013年01月05日12:26:19 於 [教育學術] 發送悄悄話 |
|
第二十二章﹕再回魔鬼聚合物
再繼續一段費根鮑姆的故事。
當時的費根鮑姆太樂觀、太自信了。當他將有關這兩個常數的論文寄給物理期刊後,兩篇文章卻都遭遇被審稿者們彈回而退稿的命運,不過,費根鮑姆並不氣餒,仍然心無旁騖,繼續深究,直到3年之後,人們對混沌現象了解更多了,思考更成熟了,學術界才逐漸認識到費根鮑姆這個工作的重要性,於是,費根鮑姆的論文得以發表,他本人也身價倍增,被曾經做過兩年臨時助理的康奈爾大學聘回去當教授。“十年寒窗無人問,一舉成名天下知”,學術界也是世俗社會的縮影,人性使然,社會現實,如此而已,毫不為怪。
林童講完了費根鮑姆的故事,大家邊聽邊議論,感慨費根鮑姆用一個簡單的計算器就作出了混沌理論中的一個重大發現。張三說,現在,計算機的圖像顯示功能這麼好,我經常把這個分岔圖放大來放大去,玩來玩去的,但對其中隱藏的這個普適規律卻熟視無睹,可見,作出科學上的重大發現,並不是一定要有最好的研究條件和設備,還是人的因素第一,重在獨立思考呀。
當費根鮑姆自己談到他的這個發現時曾經半開玩笑地說過:“我對分岔速度幾何收斂的猜想,是逼出來的。”他的意思是說,當時他的計算器算得很慢,如果想要畫出一個較為細緻的分岔圖,是不現實的。比如,像我們現在這樣,用計算機編程,對每一個離得不遠的k值,我們都要用邏輯斯蒂方程作幾百次迭代運算,才能畫出分辨率頗高的倍周期分岔圖。現在的手提電腦,完成整個計算任務,頂多幾分鐘就夠了,但用他的HP-65計算器,恐怕要算好多天。因此,費根鮑姆被‘逼’着動腦筋想辦法,因為他感興趣的只是分岔點,所以只需要在每個分岔點附近的幾個k值作迭代就可以了,並不需要對所有的k值作迭代。於是,費根鮑姆被逼着研究分岔點之間的規律,試圖從一個分岔點預言下一個分岔點的位置,這樣就可以直接跳到下一個分岔點附近作計算,大大節約運算的時間。換句話說,計算器速度太慢的困難迫使費根鮑姆領悟到並利用了分叉間距的幾何收斂性,也同時導致了費根鮑姆常數的發現。試想,如果當時費根鮑姆利用的是大型高速電子計算機,沒準兒他就與這個重大發現擦肩而過了。
開始時,費根鮑姆以為他的常數可以用別的已知常數表示出來。比如p、e……等等著名常數,但是湊了好多天也沒有湊出任何結果。費根鮑姆想,難道這是反映混沌世界出現的兩個特別常數?如果只是與有序到混沌的過程有關,那麼,除了邏輯斯蒂系統之外,在別的系統,混沌魔鬼是不是也按照這個規律出現呢?想到這兒,費根鮑姆再一次拿起了他的寶貝計算器,對另一個簡單的非線性系統(正弦映射系統):
xn+1 = k sin(xn) (22.1)
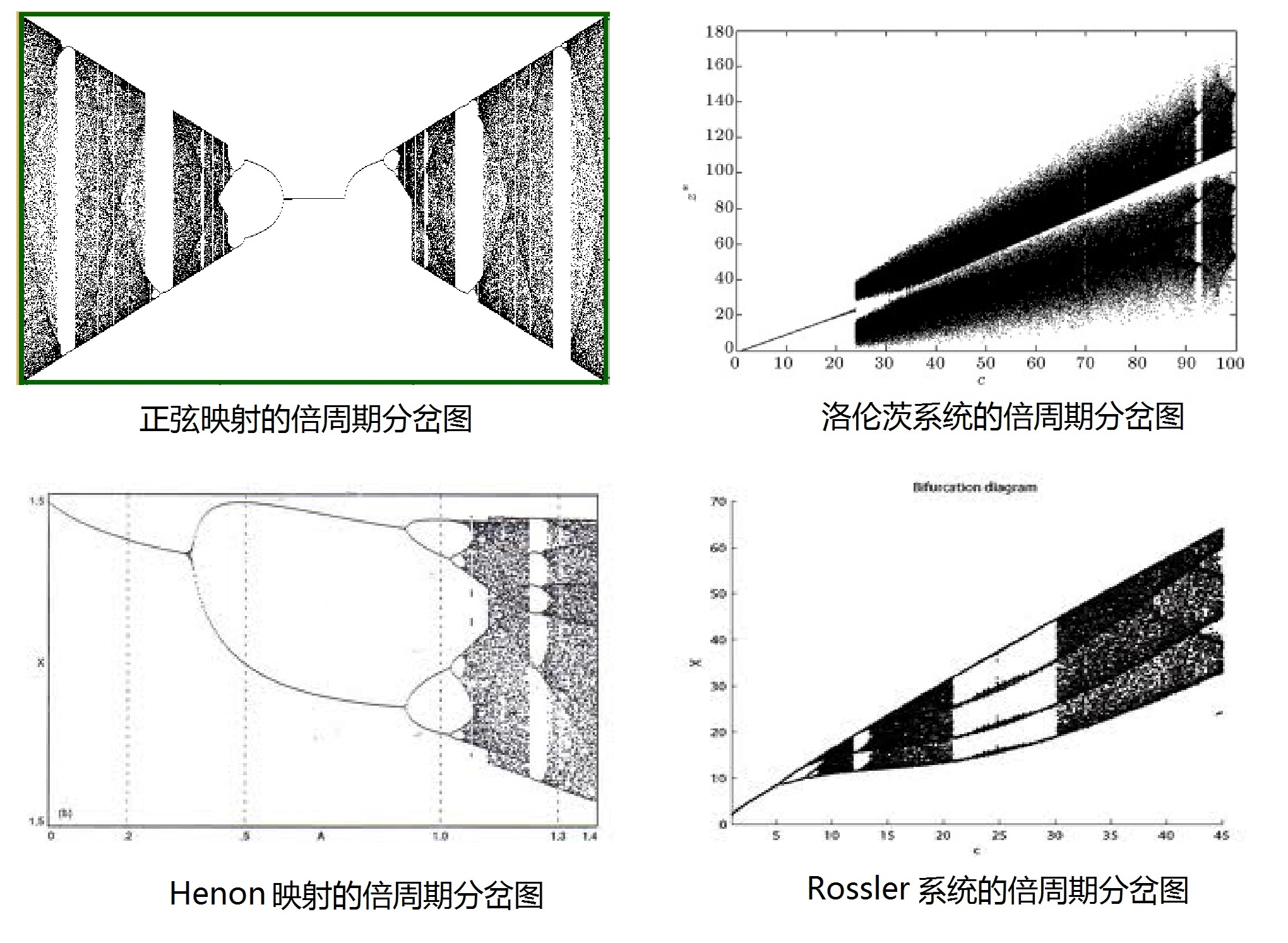
產生混沌的倍周期分岔過程作研究。 圖(22.1):更多的倍周期分岔混沌系統
對正弦映射系統倍周期分岔過程的計算結果讓費根鮑姆激動不已,因為結果表明:正弦映射系統中的混沌魔鬼,與邏輯斯蒂系統的混沌魔鬼,遵循着一模一樣的規律。它們誕生的速度比值中都有一個同樣的幾何收斂因子:
d = 4.669201609……
分岔後的寬度也和邏輯斯蒂系統的分岔寬度,遵循同樣的幾何收斂因子而減小:
α= 2.502907875……
正弦映射和邏輯斯蒂映射的迭代函數完全不一樣,一個是正弦函數,另一個邏輯斯蒂映射,是二次的拋物線函數
(xn+1= kxn·(1-xn)), (22.2)
但是,兩個系統中的混沌魔鬼卻以同樣的速度誕生!這個奇妙的事實說明,d和α兩個費根鮑姆常數與迭代函數的細節無關,它們反映的物理本質應該是只與混沌現象、或者說是只與有序到無序過渡的某種物理規律有關,這就是學術界最後所領悟到、不得不承認的“費根鮑姆常數的普適性”。簡單的HP-65計算器的確功勞不小,1982年,費根鮑姆被聘為康奈爾大學教授。1986年,費根鮑姆獲得沃爾夫物理獎,同一年,他受聘為洛克菲勒大學教授,直到如今。
之後,各行業的專家們研究了更多動力系統的倍周期分岔現象,其中包括洛倫茨系統、邏輯斯蒂系統、正弦映射、Hénon映射、Navier-Stokes映射、電子混沌電路、鐘擺等等,我們在圖(22.1)中列出了其中的一部分。人們發現,只要是通過倍周期分岔而從有序產生混沌的過程,都符合費根鮑姆常數所描述的規律。不過,對費根鮑姆常數更深一層的物理本質,似乎仍然知之甚少,科學家們仍在努力探索中。此外,從有序過渡到無序的過程,除了通過倍周期分岔之外,還有三周期分岔、多周期分岔,以及別的途徑,這些理論還不十分清楚,都有待人們去研究和發掘,這是一個值得人們去探索、耕耘的新領域。
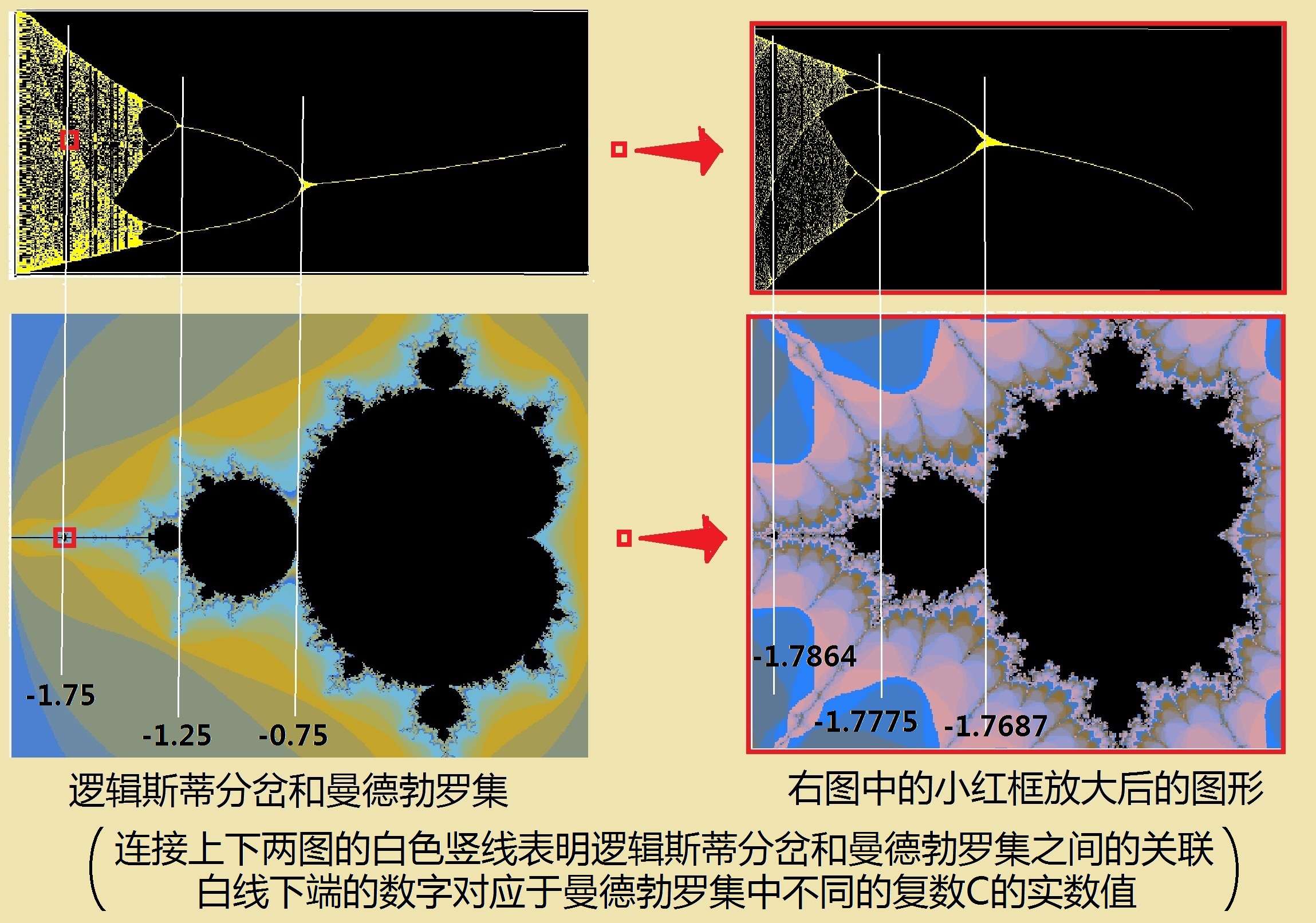
費根鮑姆常數也出現在曼德勃羅集美妙的圖形中,那個被曼德勃羅自己稱之為“魔鬼聚合物”的圖形,將邏輯斯蒂映射中的魔鬼聚合在它的實數軸上。見圖(22.2):
圖(22.2):倍周期分岔圖和曼德勃羅集
實際上,邏輯斯蒂系統的迭代方程(22.2)可以很容易地變換成同為二次函數的曼德勃羅集迭代方程:
xn+1 = xn·xn + c; (22.3)
不過這兒的c只取實數值。當c值從-2變到1/4時,用曼德勃羅集的公式(22.3)進行迭代,並將對應於每一個c值的、迭代100次到200次的結果用黃色點表示出來,便能得到如圖(22.2)左上圖所示的、和從邏輯斯蒂迭代所得到的、一模一樣的倍周期分岔圖。
圖(22.2)中連接上下兩圖的白色豎線表示邏輯斯蒂分岔和曼德勃羅集之間的關聯,白線下端的數字對應於曼德勃羅集中不同的複數C的實數值。
下一篇∶混沌到有序 |
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2012: | 再談量子力學的結論徹底粉碎了唯物主義 | |
| 2012: | 量子世界下的精神觀(I) | |
| 2011: | 為活躍論壇氣憤曬篇老文,博士別罵我抄 | |
| 2011: | 才女,看看叔叔們給你的指導 | |
| 2010: | 米笑:科學就是“毛估估” | |
| 2010: | 中國大學追求國際化的可怕誤區 | |
| 2009: | A quick word on 漢語vs. English | |
| 2009: | 學外語會扼殺人的創造性 | |
| 2008: | 九十年代的海歸易綱教授 | |