定理：在勾股定理上，周髀算经击败了欧几里德 －－ 从严格的西方学术标准而言 武士过招，用剑； 学者比高低，用理论模型。 如何用理论模型比高低？粗看，一个模型无非一堆句子：定义、假设（误译成‘公理’）、定理、推论。但透过这堆句子细看，能辨出美或丑，肤浅或深刻，笨重或优雅。当然，这视乎观者的眼光和修养（就象欣赏美女时的‘曾见沧海难为水’），但有些比较是很明显的：给定同一个现象，如果学者Ａ用了比学者Ｂ更少和更质朴的定义和假设（Ｂ的假设意味着Ａ的假设，而Ａ的假设不一定意味着Ｂ的假设），那么Ａ就打败了Ｂ。 一个好例子，就是《周髀算经》和欧几里德对勾股定理所各自提出的证明。 先看欧几里德的证明： 欧几里德的证明，若要全写出来，很长。在此只钩勒如下： Ａ、图中的粉色正方形的面积＝三角形FCB的面积的两倍； Ｂ、三角形FCB的面积＝三角形ADB的面积，因为二者全等； Ｃ、三角形ADB的面积的两倍＝图中的粉色长方形的面积。 所以，图中的粉色正方形的面积＝图中的粉色长方形的面积。 同理，图中的蓝色正方形的面积＝图中的蓝色长方形的面积。 Ｄ、粉色长方形＋蓝色长方形＝以弦为边的正方形。这与上两行结合，于是－－－ 证毕。 以上的步骤，若要真的成为证明，欧几里德需要严格地假设或定义出： 一、一个正方形的面积的算法（否则他的步骤Ａ通不过）； 二、一个任意三角形的面积的算法（否则他的步骤Ａ通不过）； 三、两个任意三角形全等的条件（否则他的步骤Ｂ通不过）； 四、一个长方形的面积的算法（否则他的步骤Ｃ通不过）； 五、假设：一个平面图形的面积＝对它作有限分割之后、各部份面积的总和（否则他的步骤Ｄ通不过）。 这里，最麻烦的是要定义一个任意三角形的面积的算法。尽管‘底乘以高除以2’这种算法看上去很直观，人类要等到最近两百年，才真正在严格意义上懂得甚么叫一般几何图形的‘面积’。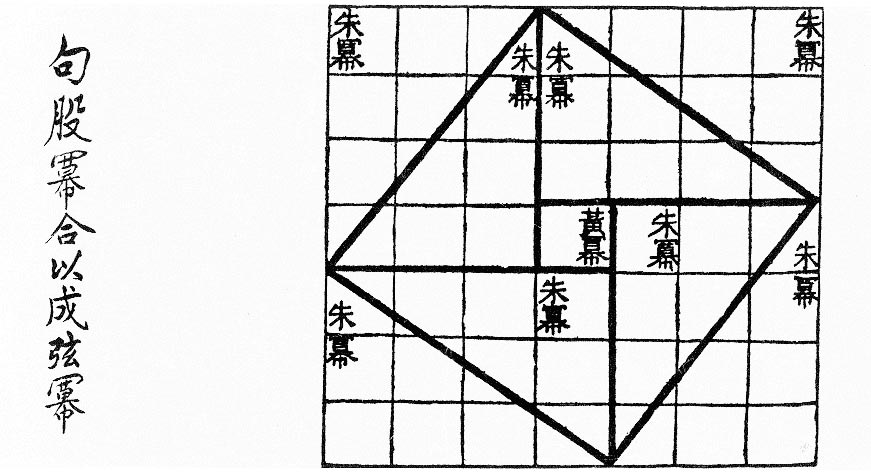 现在转头看《周髀算经》的一掌亢龙有悔： 为了清楚，把它的前后各步骤全写出来： 先玩几下拼图： Ａ、取任一直角三角形，放在上图左上角从左到右数第二个‘朱幂’的位置，叫它甲； Ｂ、取同一直角三角形的副件，以其短边贴着甲的长边，顶点重合地放在上图左上角从左到右数第三个‘朱幂’的位置，叫它乙； Ｃ、上述两三角形在‘朱幂’处的两个角是互补的（这是由Ａ和Ｂ推出的），所以在上图中、用粗线画出的四边形的顶点的内角是个直角； Ｄ、取同样步骤，用另外两个该直角三角形的副件，丙和丁，砌出上图中、用粗线画出的整个四边形，丙居右下方，丁居左下方；而且与Ｃ同理可证，此四边形每个顶点的内角都是直角； Ｅ、由于此四边形每边都是那直角三角形的弦，此四边形乃以该弦为边的正方形； 再作两个关键的图形重组： Ｆ、把乙搬到甲的左上面、图中左上角‘朱幂’的位置，与甲拼成一竖放的长方形（之所以是长方形，是因为两三角形相贴的两内角互补）； Ｇ、把丙搬到丁的左下面、图中左下角‘朱幂’的位置，与丙拼成一横卧的长方形（之所以是长方形，是因为相贴的两内角互补）； 最后，在视角上的作一飞跃： Ｈ、以直角三角形的弦为边的正方形（图中粗线界定者）＝Ｆ和Ｇ两步所述的两个长方形 加上 图中央的‘黄幂’； Ｉ、上述等式的右方＝以直角三角形的短边为边的正方形 加上 以直角三角形的长边为边的正方形； 所以，以弦为边的正方形的面积＝以短边为边的正方形的面积＋以长边为边的正方形的面积， 证毕。 要把以上各步变成一个证明，《周髀算经》只需如下的定义或假设： 一、上列的欧几里德的条件一（一个正方形的面积的算法）； 二、上列的欧几里德的条件四（一个长方形的面积的算法）； 三、上列的欧几里德的条件五（一个平面图形的面积＝对它作有限分割之后、各部份面积的总和；《周髀算经》在上面的拼图游戏，用的就是这一假设；可称之为‘定理氏所蒸馏出来之拼图公理’，哈）。 妙就妙在，《周髀算经》根本不须欧几里德的条件二和三。既不用假设甚么叫三角形全等，更不用涉足一般图形的面积的算法、这个要用到现代量度理论才能弄得清的泥潭。 所以，为了同样的收益（勾股定理），欧几里德付出了五个条件的代价，其中一个（‘面积的算法’）还挺昂贵，而《周髀算经》只用了这五个条件中最不昂贵的三个。 二者高下立见。 故本定理曰：周髀算经 克 欧几里德 于 勾股定理。