| 【数学】实用的拉丁方 |
| 送交者: gugeren 2017年05月25日09:53:17 于 [教育学术] 发送悄悄话 |
|
【数学】实用的拉丁方 提起拉丁方(Latin square),做过药物实验设计的网友应该对它不陌生。 拉丁方(阵)是一种 n × n 的方阵。在这种 n × n 的方阵里,拥有 n 种不同的元素,每一种不同的元素在同一行或同一列里仅出现1次。 【图1:拉丁方】
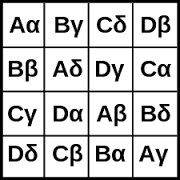
实际上,人们在实际生活中使用的,是拉丁方的一种特殊形式,称“正交拉丁方(orthogonal Latin square)”。 正交拉丁方,学名是“希腊拉丁方(Graeco Latin square)”。这样的拉丁方内,至少由2个不同的字符、颜色或字体等组合成为方阵内的每个元素,而且没有同样的元素组合会出现在同一个拉丁方内。 【图2:正交拉丁方】
正交拉丁方可用于科学实验的设计和体育赛程的编排。 欧拉在研究了拉丁方以及正交拉丁方以后,他证明了: 1】不存在2-阶正交拉丁方。 2】当n为奇数,或n为4的倍数时,存在正交n-阶拉丁方。 3】剩下则是2倍奇数阶的正交拉丁方:6, 10, 14, 18, ...。 可以看出,欧拉解决了所有自然数阶的正交拉丁方的四分之三的内容。 由于欧拉费尽心机制作不出6阶的正交拉丁方,他推测不存在6阶的正交拉丁方,从而又引申出不存在所有的3】的情况。 但是,这次欧拉的猜测是错误的。 1901年,法国数学家Gaston Tarry(1843-1931)证明了6阶正交拉丁方不存在。 1960年,3位美国数学家Ernest Tilden Parker(1926-1991),Raj Chandra Bose(1901-1987)和Sharadchandra Shankar Shrikhande(1917-)证明了存在除了6阶以外的所有2倍奇数阶的正交拉丁方。 更加复杂的正交拉丁方还有: 相互正交拉丁方(Mutually orthogonal Latin squares) 【图3:Mutually orthogonal Latin squares】
== 相关链接: 拉丁方: https://en.wikipedia.org/wiki/Latin_square 正交(希腊)拉丁方: https://en.wikipedia.org/wiki/Graeco-Latin_square 相互正交拉丁方: https://en.wikipedia.org/wiki/Graeco-Latin_square#Mutually_orthogonal_Latin_squares |
|
 |
 |
| 实用资讯 | |
|
|
| 一周点击热帖 | 更多>> |
| 一周回复热帖 |
| 历史上的今天:回复热帖 |
| 2016: | 中国通:习近平似蒋介石(命运也将一样 | |
| 2016: | 推背图第四四象所说的圣人就是在芬兰的 | |
| 2015: | 范例世界-从“经验与知识同一”说起(C) | |
| 2015: | 一位小学生天天看《新闻联播》,竟然写 | |
| 2014: | 美国小孩为什么学不好英文 | |
| 2013: | c_y_lo, 请教个英语问题 | |
| 2013: | 范例哲学如何解决笛卡尔的“心灵-身体 | |
| 2012: | 亲子相认是基本的人性 | |
| 2012: | 马寅初有两妻七孩,是个口是心非的不良 | |