| 565、微观粒子的身份证—薛定谔方程(四) |
| 送交者: 和颜清心 2018年12月01日01:17:58 于 [教育学术] 发送悄悄话 |
|
微观粒子的身份证—— 薛定谔方程(四) 朋友,现在我们已经了解了‘薛定谔方程’的外表, 并且知道‘薛方程’是微观粒子的‘说明书’、 该‘方程’也是科学家进入微观世界的‘入场卷’, ‘说明书’是用数学形式写的, 那些生疏的符号,令人茫然……。 下面就让我们以某些可接受的形式做跳板, 以迂回的方法,渐渐靠近这个深不可测的方程吧。
朋友,现在您是否已经了解, 微观粒子不像小球那样是一个可见粒子? 就像我们的身体, 虽然其间充满了无数微观粒子, 可是我们能看见它们吗? 不能! 我们看见的只有包裹着灵魂的皮肤或肌肉。 每天、每天、 日复一日、年复一年, 从太阳升起,到日薄西山, 我们几乎无时无刻 让这些可见的东东,牵着鼻子走, 一会儿心生愤怒去骂人、 一会儿又对财富生出无限贪爱……, 咳,某的贪心尤其严重, 期盼终有一天 那圣洁的清净会早日到来……。
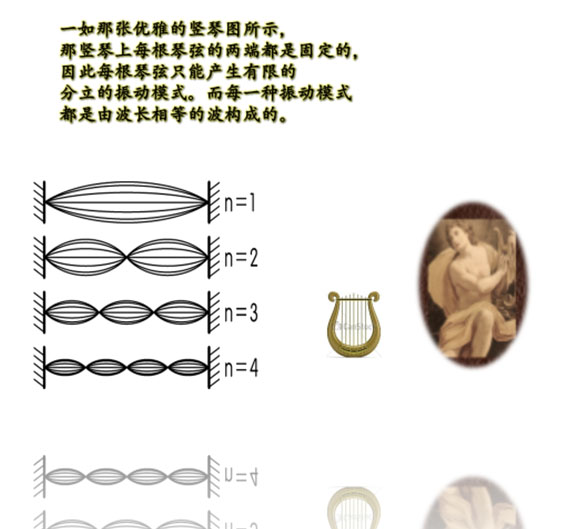
话说, 微观粒子的本质是波动性, 现在就让我们来看看 ‘波动’中的“驻波”是个什么东东。 先来看一幅名画—— “太阳神和他的七弦琴”。 想象一曲超凡脱俗的天籁之音袅袅飘来, 妙音萦绕耳畔,给人带来无限喜悦…。
我们说如果 n=1的波长是“基波”, 那么, n=2或n=3的波长, 相对来说,就是较短的波了。 (琴弦的波动可产生“谐波”*。通俗些说, 谐波是指波动中所含频率 是基波频率整数倍的那些部分。)
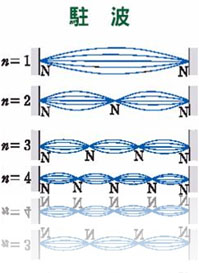
我们知道 两端固定的弦,它的震荡可以形成‘驻波’, 而琴弦的总长度是驻波内波长的整数倍。
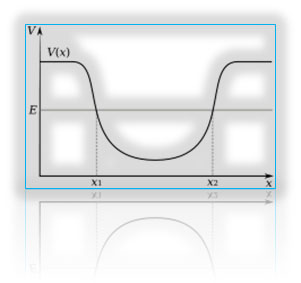
‘电子’等微粒的波动, 就其被束缚的特性来说, 正像太阳神七弦琴的琴弦, 那些由粒子的负电或正电构成的“电场”(“电势场”), 就是一个个束缚电子微粒的“阱” (阱,读作“井”,‘陷坑’的意思)。
势阱,具有‘井’的态势。 这种情势,正像前面的彩图所示: 两边陡峭的坡道, 限制着“人与车的组合”, 在两点之间运动; 或者 如图中阿波罗手中的七弦琴: 琴弦的两端固定着2个点, 限制着琴弦 在这个距离间来回振动。
原子的电场(势阱), 同样决定了其间的电子 只能具有 有限多个‘能级’ 或运行的痕迹。 比如, n=1是波长最长的‘基态’,那么 n=2、n=3……等的波长 就是越来越短的后续的‘激发态’, 每一种定态都严格符合“有限多个” 和“份量相等”的量子化特征。
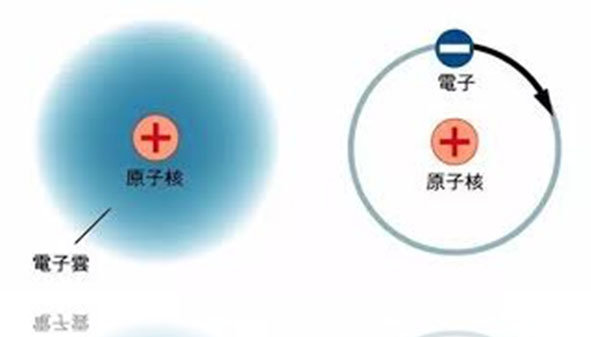
严格地说, 电子没有像宏观粒子那样的运行轨道。 电子的运行痕迹, 可以像二条首尾相接的弦, 是由有限的波长构成的, 电子的运行痕迹,表示的是它们的能量的不同 及其振幅、波长和频率的不同。 可以想像,那些无形的电子的“运行痕迹”, 实际是包含着电子的波动的。
【说明】
1926年薛定谔对电子运动做了数学处理, 提出著名的薛定谔方程。 这个方程如果用‘三维坐标’的图形来表示的话, 就是‘电子云’。
谢谢。 |
|
 |
 |
| 实用资讯 | |
|
|
| 一周点击热帖 | 更多>> |
| 一周回复热帖 |
| 历史上的今天:回复热帖 |
| 2017: | (9)为什么我对中国文化持基本否定态度 | |
| 2017: | 彭运生谈艺录(140) | |
| 2016: | 劫困济贫的欧巴马健保:抢了彼德付保罗 | |
| 2016: | 2017银河少儿剧团演出公告(学戏剧认汉 | |
| 2015: | 感恩的第一天 | |
| 2015: | 87.菩萨的粗细智境 | |
| 2013: | 日本二战投降书原件复印,明确日要遵守 | |
| 2013: | 关于范例学本体论的概念的解释(4) | |