定理:在勾股定理上,周髀算經擊敗了歐幾里德 -- 從嚴格的西方學術標準而言
武士過招,用劍;
學者比高低,用理論模型。
如何用理論模型比高低?粗看,一個模型無非一堆句子:定義、假設(誤譯成‘公理’)、定理、推論。但透過這堆句子細看,能辨出美或丑,膚淺或深刻,笨重或優雅。當然,這視乎觀者的眼光和修養(就象欣賞美女時的‘曾見滄海難為水’),但有些比較是很明顯的:給定同一個現象,如果學者A用了比學者B更少和更質樸的定義和假設(B的假設意味着A的假設,而A的假設不一定意味着B的假設),那麼A就打敗了B。
一個好例子,就是《周髀算經》和歐幾里德對勾股定理所各自提出的證明。
先看歐幾里德的證明:

歐幾里德的證明,若要全寫出來,很長。在此只鈎勒如下:
A、圖中的粉色正方形的面積=三角形FCB的面積的兩倍;
B、三角形FCB的面積=三角形ADB的面積,因為二者全等;
C、三角形ADB的面積的兩倍=圖中的粉色長方形的面積。
所以,圖中的粉色正方形的面積=圖中的粉色長方形的面積。
同理,圖中的藍色正方形的面積=圖中的藍色長方形的面積。
D、粉色長方形+藍色長方形=以弦為邊的正方形。這與上兩行結合,於是---
證畢。
以上的步驟,若要真的成為證明,歐幾里德需要嚴格地假設或定義出:
一、一個正方形的面積的算法(否則他的步驟A通不過);
二、一個任意三角形的面積的算法(否則他的步驟A通不過);
三、兩個任意三角形全等的條件(否則他的步驟B通不過);
四、一個長方形的面積的算法(否則他的步驟C通不過);
五、假設:一個平面圖形的面積=對它作有限分割之後、各部份面積的總和(否則他的步驟D通不過)。
這裡,最麻煩的是要定義一個任意三角形的面積的算法。儘管‘底乘以高除以2’這種算法看上去很直觀,人類要等到最近兩百年,才真正在嚴格意義上懂得甚麼叫一般幾何圖形的‘面積’。
現在轉頭看《周髀算經》的一掌亢龍有悔:
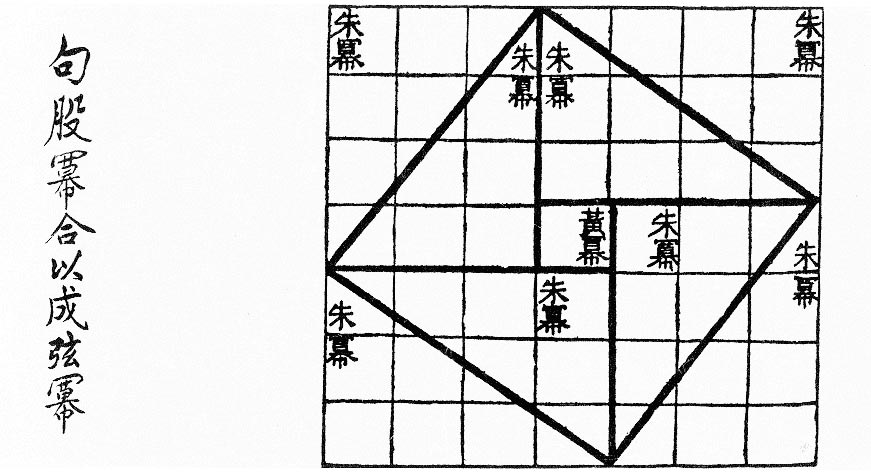
為了清楚,把它的前後各步驟全寫出來:
先玩幾下拼圖:
A、取任一直角三角形,放在上圖左上角從左到右數第二個‘朱冪’的位置,叫它甲;
B、取同一直角三角形的副件,以其短邊貼着甲的長邊,頂點重合地放在上圖左上角從左到右數第三個‘朱冪’的位置,叫它乙;
C、上述兩三角形在‘朱冪’處的兩個角是互補的(這是由A和B推出的),所以在上圖中、用粗線畫出的四邊形的頂點的內角是個直角;
D、取同樣步驟,用另外兩個該直角三角形的副件,丙和丁,砌出上圖中、用粗線畫出的整個四邊形,丙居右下方,丁居左下方;而且與C同理可證,此四邊形每個頂點的內角都是直角;
E、由於此四邊形每邊都是那直角三角形的弦,此四邊形乃以該弦為邊的正方形;
再作兩個關鍵的圖形重組:
F、把乙搬到甲的左上面、圖中左上角‘朱冪’的位置,與甲拼成一豎放的長方形(之所以是長方形,是因為兩三角形相貼的兩內角互補);
G、把丙搬到丁的左下面、圖中左下角‘朱冪’的位置,與丙拼成一橫臥的長方形(之所以是長方形,是因為相貼的兩內角互補);
最後,在視角上的作一飛躍:
H、以直角三角形的弦為邊的正方形(圖中粗線界定者)=F和G兩步所述的兩個長方形 加上 圖中央的‘黃冪’;
I、上述等式的右方=以直角三角形的短邊為邊的正方形 加上 以直角三角形的長邊為邊的正方形;
所以,以弦為邊的正方形的面積=以短邊為邊的正方形的面積+以長邊為邊的正方形的面積,
證畢。
要把以上各步變成一個證明,《周髀算經》只需如下的定義或假設:
一、上列的歐幾里德的條件一(一個正方形的面積的算法);
二、上列的歐幾里德的條件四(一個長方形的面積的算法);
三、上列的歐幾里德的條件五(一個平面圖形的面積=對它作有限分割之後、各部份面積的總和;《周髀算經》在上面的拼圖遊戲,用的就是這一假設;可稱之為‘定理氏所蒸餾出來之拼圖公理’,哈)。
妙就妙在,《周髀算經》根本不須歐幾里德的條件二和三。既不用假設甚麼叫三角形全等,更不用涉足一般圖形的面積的算法、這個要用到現代量度理論才能弄得清的泥潭。
所以,為了同樣的收益(勾股定理),歐幾里德付出了五個條件的代價,其中一個(‘面積的算法’)還挺昂貴,而《周髀算經》只用了這五個條件中最不昂貴的三個。
二者高下立見。
故本定理曰:周髀算經 克 歐幾里德 於 勾股定理。
 為了清楚,把它的前後各步驟全寫出來:
先玩幾下拼圖:
A、取任一直角三角形,放在上圖左上角從左到右數第二個‘朱冪’的位置,叫它甲;
B、取同一直角三角形的副件,以其短邊貼着甲的長邊,頂點重合地放在上圖左上角從左到右數第三個‘朱冪’的位置,叫它乙;
C、上述兩三角形在‘朱冪’處的兩個角是互補的(這是由A和B推出的),所以在上圖中、用粗線畫出的四邊形的頂點的內角是個直角;
D、取同樣步驟,用另外兩個該直角三角形的副件,丙和丁,砌出上圖中、用粗線畫出的整個四邊形,丙居右下方,丁居左下方;而且與C同理可證,此四邊形每個頂點的內角都是直角;
E、由於此四邊形每邊都是那直角三角形的弦,此四邊形乃以該弦為邊的正方形;
再作兩個關鍵的圖形重組:
F、把乙搬到甲的左上面、圖中左上角‘朱冪’的位置,與甲拼成一豎放的長方形(之所以是長方形,是因為兩三角形相貼的兩內角互補);
G、把丙搬到丁的左下面、圖中左下角‘朱冪’的位置,與丙拼成一橫臥的長方形(之所以是長方形,是因為相貼的兩內角互補);
最後,在視角上的作一飛躍:
H、以直角三角形的弦為邊的正方形(圖中粗線界定者)=F和G兩步所述的兩個長方形 加上 圖中央的‘黃冪’;
I、上述等式的右方=以直角三角形的短邊為邊的正方形 加上 以直角三角形的長邊為邊的正方形;
所以,以弦為邊的正方形的面積=以短邊為邊的正方形的面積+以長邊為邊的正方形的面積,
證畢。
要把以上各步變成一個證明,《周髀算經》只需如下的定義或假設:
一、上列的歐幾里德的條件一(一個正方形的面積的算法);
二、上列的歐幾里德的條件四(一個長方形的面積的算法);
三、上列的歐幾里德的條件五(一個平面圖形的面積=對它作有限分割之後、各部份面積的總和;《周髀算經》在上面的拼圖遊戲,用的就是這一假設;可稱之為‘定理氏所蒸餾出來之拼圖公理’,哈)。
妙就妙在,《周髀算經》根本不須歐幾里德的條件二和三。既不用假設甚麼叫三角形全等,更不用涉足一般圖形的面積的算法、這個要用到現代量度理論才能弄得清的泥潭。
所以,為了同樣的收益(勾股定理),歐幾里德付出了五個條件的代價,其中一個(‘面積的算法’)還挺昂貴,而《周髀算經》只用了這五個條件中最不昂貴的三個。
二者高下立見。
故本定理曰:周髀算經 克 歐幾里德 於 勾股定理。
為了清楚,把它的前後各步驟全寫出來:
先玩幾下拼圖:
A、取任一直角三角形,放在上圖左上角從左到右數第二個‘朱冪’的位置,叫它甲;
B、取同一直角三角形的副件,以其短邊貼着甲的長邊,頂點重合地放在上圖左上角從左到右數第三個‘朱冪’的位置,叫它乙;
C、上述兩三角形在‘朱冪’處的兩個角是互補的(這是由A和B推出的),所以在上圖中、用粗線畫出的四邊形的頂點的內角是個直角;
D、取同樣步驟,用另外兩個該直角三角形的副件,丙和丁,砌出上圖中、用粗線畫出的整個四邊形,丙居右下方,丁居左下方;而且與C同理可證,此四邊形每個頂點的內角都是直角;
E、由於此四邊形每邊都是那直角三角形的弦,此四邊形乃以該弦為邊的正方形;
再作兩個關鍵的圖形重組:
F、把乙搬到甲的左上面、圖中左上角‘朱冪’的位置,與甲拼成一豎放的長方形(之所以是長方形,是因為兩三角形相貼的兩內角互補);
G、把丙搬到丁的左下面、圖中左下角‘朱冪’的位置,與丙拼成一橫臥的長方形(之所以是長方形,是因為相貼的兩內角互補);
最後,在視角上的作一飛躍:
H、以直角三角形的弦為邊的正方形(圖中粗線界定者)=F和G兩步所述的兩個長方形 加上 圖中央的‘黃冪’;
I、上述等式的右方=以直角三角形的短邊為邊的正方形 加上 以直角三角形的長邊為邊的正方形;
所以,以弦為邊的正方形的面積=以短邊為邊的正方形的面積+以長邊為邊的正方形的面積,
證畢。
要把以上各步變成一個證明,《周髀算經》只需如下的定義或假設:
一、上列的歐幾里德的條件一(一個正方形的面積的算法);
二、上列的歐幾里德的條件四(一個長方形的面積的算法);
三、上列的歐幾里德的條件五(一個平面圖形的面積=對它作有限分割之後、各部份面積的總和;《周髀算經》在上面的拼圖遊戲,用的就是這一假設;可稱之為‘定理氏所蒸餾出來之拼圖公理’,哈)。
妙就妙在,《周髀算經》根本不須歐幾里德的條件二和三。既不用假設甚麼叫三角形全等,更不用涉足一般圖形的面積的算法、這個要用到現代量度理論才能弄得清的泥潭。
所以,為了同樣的收益(勾股定理),歐幾里德付出了五個條件的代價,其中一個(‘面積的算法’)還挺昂貴,而《周髀算經》只用了這五個條件中最不昂貴的三個。
二者高下立見。
故本定理曰:周髀算經 克 歐幾里德 於 勾股定理。







