| 天蓉:《走近混沌》-1-從分形龍談起 |
| 送交者: 天蓉 2012年08月13日13:33:22 於 [教育學術] 發送悄悄話 |
|
《走近混沌》
混沌是什厶?要理解混沌的概念,最好先理解分形。分形是什厶?要理解分形,最好首先從一個例子說起。那就讓我們從一個不算很複雜,也不算很簡單的分形的例子∶分形龍說起吧。
第一章∶有趣的分形龍
拿着一條細長的紙帶,把它朝下的一頭拿上來,與上面的一頭併到一起。用一句簡單的話說,就是將紙帶對摺。接着,把對摺後的紙帶再對摺,又再對摺,重複這樣的對摺幾十次┅┅
然後,鬆開紙帶,從紙帶側面看過去,如圖(1.1)所示,我們得到是一條彎彎曲曲的折線。請別小看這個連小孩子都會做的遊戲。從它開始,我們可以探索一連串現代科技中耳熟能詳的名詞∶分形、混沌、蝴蝶效應、生命產生、系統科學┅┅
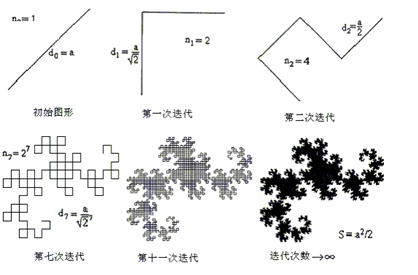
我們把‘紙帶對摺一次’的動作,用數學的語言來表述,它對應於幾何圖形的一次‘迭代’。如剛才所描述的紙帶‘對摺’那種循環往復的‘迭代’操作,所得到的最終圖形叫做中國龍,或稱分形龍。圖(1.2)描述了分形龍曲線的幾何圖形生成過程∶
圖(1.2)分形龍曲線的生成過程
仔細研究圖(1.2)中分形龍的產生過程,可觀察到如下三個有趣之處: 1. 簡單的迭代,進行多次之後,產生了越來越複雜的圖形; 2. 越來越複雜的圖形表現出一種‘自相似性’; 3. 迭代次數較少時,曲線看起來是一維折線,此曲線隨着迭代次數的增加而逐漸充滿部分平面。
第一條特點一目了然,無需多言。
第二條的‘自相似性’是什厶意思呢?那是說∶一個圖形的自身可以看成是由許多與自己相似的,大小不一的部分組成的。最通俗的‘自相似’例子是中國人喜歡吃的花菜,花菜的每一部分,都可以看成是與整棵花菜結腹相似的‘小花菜’。分形龍曲線也具有這種‘自相似性’,從圖(1.3)可以看出∶分形龍可以看成是由四個更小的但形狀完全一樣的‘小分形龍’組成的。
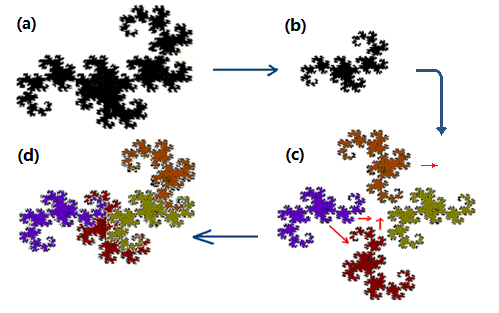
圖(1.3)分形龍的自相似性
圖(1.3a)是分形龍原來的圖形。我們將(a)圖縮小二分之一,得到為原來大小一半的圖(b);然後,圖形(c)包含了四個不同方向的小圖形;將這4個小圖按照紅色箭頭的方向移動後,把它們拼成如圖(d)的形狀,可以看出,圖(d)是和原圖(a)一模一樣的圖形。
我們再回到圖(1.2),分形龍曲線的生成過程。上面說到了,這個分形龍曲線生成過程的第三條特點是有關圖形維數的變化。隨着迭代次數的增加,一維的折線逐漸充滿部分平面,看起來好像變成了一個二維圖形。
這兒談到了幾何圖形的‘維數’,維數是一個嚴格的數學概念,我們不應該只憑感覺了,需要更多的數學論證。也就是說,我們需要仔細研究研究,當迭代的次數增加下去,趨向於無窮的時候,分形龍曲線的維數到底是多少呢?
有人,比如張三,思維比較經典,可能會說,分形龍是由一條紙帶反覆摺疊而成的。在數學上,就是一條直線段反覆摺疊而成的。摺疊再多的次數,圖形依然是由一條一條小小的“線段”腹成的,仍然是“線”,當然還是個“一維圖形”嘍!
但李四觀察得更細緻些,他反駁張三說,事情可不是那厶簡單。凡事涉及到了‘無限’,就可能得到一些你意料之外的結果。比如,就拿你剛才說到的‘一條一條小線段’ 來說吧,我們可以研究,當直線摺疊下去時,這每條小線段的長度d(圖中所示的d1,d2┅┅dn)。如圖(1.2)所示,很容易看出來,d會越來越小、越來越小。當n趨於無窮時,d會趨於0。也就是說,每一小段的長度都是0。儘管到了最後,每條小線段的長度都是0,但整條直線的長度卻顯然不是0。這原因就是因為有無限多個小線段加起來的緣故。事實上,可以證明,這無限多個長度為0的小線段加起來,結果的總長度不但不是0,還是趨於無窮大!因此,李四說,照我看來,當這條直線無限摺疊下去時,每個小線段變成了一個點,這些點充滿了分形龍圖形所在的那塊平面,最終的分形龍,應該等效於一個二維圖形!
分形龍到底是一維圖形,還是二維圖形呢?正當張三和李四各執己見,爭論不休時,一旁站着的王二發言了,他的觀點更是不同凡響∶
“這分形龍的維數,為什厶一定要是你們兩人所說的,或者1、或者2呢?難道它就不能是個1.5,1.8,或者是二分之三這樣的分數嗎?”
維數是個分數!那是什厶意思啊?張三李四都沒聽過,其實王二也只是如此猜想而已,並不了解是否真有‘分數維’這一說。於是,這個既簡單又複雜的美妙的分形龍圖形,激發了他們的好奇心和求知慾。這三個大學校園結交的好朋友∶學工程的張三,物理系的李四,以及學生物的王二,開始了一趟幾何之旅。他們對分數維圖形,也就是‘分形’,從不同的角度進行了進一步的探索。
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | “只賣出了一本” | |
| 2011: | 與中科院的研究員們笑談民科現象 | |
| 2010: | 哪位能總結總結你們討論了什麼? | |
| 2010: | 論鬼神在人類進化、歷史發展、政治進程 | |
| 2008: | 關於PRL黑幕請教本壇大佬 | |
| 2008: | 好戲開鑼,方舟子PK施一公。 | |