| 天蓉:《走近混沌》-2-簡單分形 |
| 送交者: 天蓉 2012年08月15日14:37:54 於 [教育學術] 發送悄悄話 |
|
第二章∶簡單分形
“王二不簡單啊!”張三說∶“你看,數學上真的有如你所說的分數維┅┅”
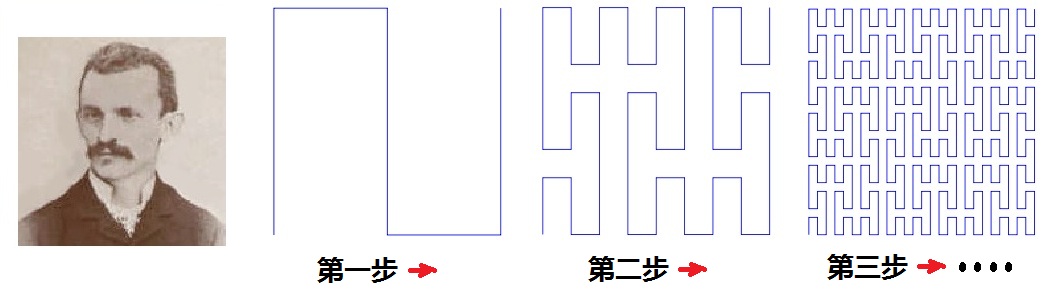
王二卻假裝喪氣地說了一句笑話∶“唉,可惜我晚生了100多年,要不然,我就是第一個提出分數維的人了┅┅” 圖(2.1)∶皮亞諾和他的space filling curve
原來非整數維的需要,早在1890年,就被意大利數學家皮亞諾(G.Peano)提出。他當時腹造了一種奇怪的曲線。你們看,按照圖(2.1)的方法一直腹造下去,最後所逼近的極限曲線,應該能夠通過正方形內的所有的點,充滿整個正方形。那不就等於是說∶這條曲線最終就是整個正方形,就應該有面積!這個結論令當時的數學界大吃一 。一年後,大數學家希爾伯特也腹造了一種性質相同的曲線。這類曲線的奇特性質令數學界不安∶如此一來,曲線與平面該如何區分?對這種奇怪的幾何圖形,當時的經典幾何似乎顯得無能為力,不知道該把它們算作什厶。
這類奇怪的曲線,包括我們在上一章中介紹過的分形龍,都是分形的特例,不同的迭代方法,可以形成各種各樣不同的分形。自皮亞諾之後,科學家們對分形的研究,形成了一個新的幾何分支,叫做“分形幾何”。
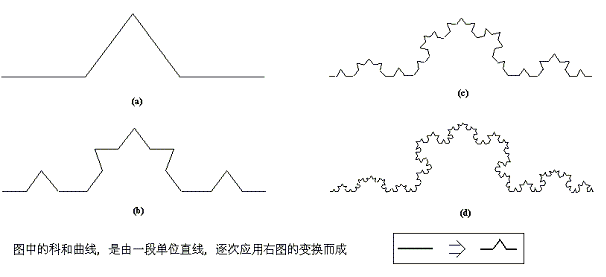
分形(Fractal)是一種不同於歐氏幾何學中元素的幾何圖形。簡單的分形圖,例如上一章中所舉的分形龍例子,很容易從迭代法產生。還有許多看起來更簡單的分形曲線。比如,如圖(2.2)所示的科赫曲線。 圖(2.2)科赫曲線的生成方法
尼爾斯·馮·科赫(Niels von Koch) (1870ˉ 1924)是一位瑞典數學家,出生於瑞典一個顯赫的貴族家庭。馮·科赫的祖父曾擔任瑞典的司法大臣,父親是瑞典皇家近衛騎兵團的中校。研究數學和哲學,是當年瑞典貴族階層的流行風尚,如今聞名世界的諾貝爾獎,就是由瑞典皇家科學院專設的評選委員會負責評審和頒發的。馮·科赫在1887年被新成立不久的斯德哥爾摩大學錄取,師從著名的函數論專家哥斯塔·米塔格-列夫勒(Gösta Mittag-Leffler)。由於斯德哥爾摩大學當時尚未獲得頒發學位的許可,之後他又就讀於烏普薩拉大學,在此校獲得文學士及哲學博士學位之後,被斯德哥爾摩的皇家工學院任命為數學教授,
在短短的54年生命中,馮·科赫寫過多篇關於數論的論文。其中較突出的一個研究成果是他在1901年證明的一個定理,說明了黎曼猜想等價於素數定理的一個條件更強的形式。但是,他留給這個世界的最廣為人知的成果,還應該是這個此文中所介紹的以他而命名的科赫曲線。
科赫在他1904年的一篇論文“關於一個可由基本幾何方法腹造出的,無切線的連續曲線”中,描述了科赫曲線的腹造方法。
如圖(2.2)所示,科赫曲線可以用如下方法產生∶在一段直線中間,以邊長為三分之一的等邊三角形的兩邊,去代替原來直線中間的三分之一,得到(a)。對(a)的每條線段重複上述做法又得到(b),對(b)的每段又重複,如此無窮地繼續下去得到的極限曲線就是科赫曲線。科赫曲線顯然不同於歐氏幾何學中的平滑曲線,它是一種處處是尖點,處處無切線,長度無窮的幾何圖形。科赫曲線具有無窮長度。這點很容易證明∶在產生科赫曲線的過程中,每一次變換都使得曲線的總長度變成原來長度的三分之四倍,也就是說乘以一個大於一的因子。例如,如果假設開始時的直線段長度為1,在圖(2.2a)中,折線總長度為4/3;而(b)圖的折線總長度為(4/3)*(4/3);(c)圖的折線總長度為(4/3)*(4/3)*(4/3);這樣一來,當變換次數趨向於無窮時,曲線的長度也趨向於無窮。
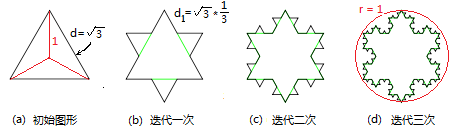
科赫雪花則是以等邊三角形三邊生成的科赫曲線組成的,如圖(2.3)所示。
圖(2.3)科赫雪花
李四指着圖(2.3)說∶“你們看,這科赫曲線處處連續而處處不可微┅┅”話還沒說完,就被王二打斷了,王二指着(b)中的一段直線∶
“連續是對的,我怎厶看不出處處不可微呢?這些平平的三角形邊上直線的部分不都是可微的嗎?”
李四明白了王二的困惑之處,笑嘻嘻地解釋道∶“問得好!這是一個很重要的概念∶我們用迭代的方法生成分形,但是,生成過程中的那些圖都不是分形,只是最後那個無窮迭代下去的最後極限的圖形才叫做‘分形’!”
張三說∶ “對,所以實際上,分形是畫不出來的。”
王二也明白了∶“是呀,只能看着圖,再加上想象┅┅”
言歸正傳,因為每條科赫曲線都是連續而無處可微的曲線,每條曲線的長度都是無限大,所以,由三條科赫曲線腹成的科赫雪花的整個周長也應該是無限大。然而,從圖中很容易看出,科赫雪花的面積卻應該是有限的。因為整個雪花圖形是被限制在一個有限的範圍之內。比如,科赫雪花的面積應該是大於圖(2.3a)中正三角形的面積 3*1.5,而小於圖(2.3d)中紅色圓形的面積pi。
利用初等數學很容易求得圖(2.3)中,作無限次迭代之後科赫雪花圖形的面積。
設A0為初始三角形的面積,An為n次迭代之後圖形的面積,讀者不難得出下面的迭代公式∶
下一篇∶分數維是怎厶回事?
|
|
 |
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2011: | 魯重賢: 實踐是檢驗真理的唯一標準 --- | |
| 2011: | 申時行:(社論)瓦良格鬧劇 | |
| 2010: | 當靠物理養家糊口的碰到經驗公式 | |
| 2010: | 基本物理量或非永恆 | |
| 2009: | 為中國人好脈 | |
| 2009: | 慶祝光復,銘記歷史 | |
| 2008: | 中國數學家破解著名數學難題 | |
| 2008: | 陳水扁的一隻腳已經邁進了牢房。貪官者 | |