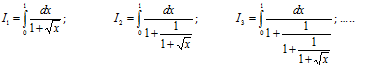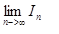| 積分智力題試解 (修改) |
| 送交者: 粱遠聲 2017年08月11日16:35:12 於 [靈機一動] 發送悄悄話 |
|
定義:
求
積分智力題試解 先討論被積函數的分母。f1(x) = 1 + x^0.5, f2(x) = 1 + 1/f1(x), f3(x) = 1 + 1/f2(x), fn+1(x) = 1 + 1/fn(x) fn(x) > 1 fn+1(x) - fn-1(x) = 1 + 1/(1+1/fn-1(x)) - fn-1(x) = (1 - fn-1(x) - fn-1^2(x))/(fn-1(x) + 1) < 0 這樣我們得到 fn+1(x) < fn-1(x) (1) fn(x) > 1 (2) (1) 說明x在(0,1) 區間奇數列單調減少,偶數列單調減少。(2)說明數列有下界。所以奇數列收斂,偶數列收斂。接下來看看數列的極限是什麼。在(0,1) 區間任取x0, 假設奇數列收斂於a, 根據遞推公式 fn+1(x0) = 1 + 1/(1+1/fn-1(x0)) (3) 得到 a = 1 + 1/(1+1/a) (4) 解得 a = (1+5^0.5)/2 (5) (3)也是偶數列的遞推公式,所以(5) 也是偶數列的極限值。奇偶列收斂於同一個極限,推出 fn(x0) 收斂。由於x0的任意性,fn(x) 收斂於常數 a。 所以 In 收斂於 1/a |
|
|
 | |
|
 |
| 實用資訊 | |