朋友们都知道我数学好,经常有来咨询的,曾经有人(高中生)来问群论。当太太听我简介这群论是何方神圣后,不禁问了一句,如果家长找不到人问怎么办。
我最要好的一位朋友却是很客气,儿子念初中、高中,从未来问过。终于有一次,他问了我一道平面几何题。一圆直径为3,在同一直径上,又并排放了两个圆,直径分别为2和1。现有第四个圆。在大圆之内,但两个小圆之外,与三个圆均相切。问第四个圆直径为何?
思考良久,未能突破,只得投降。以后,就再没敢对他说“有数学问题来问我。”
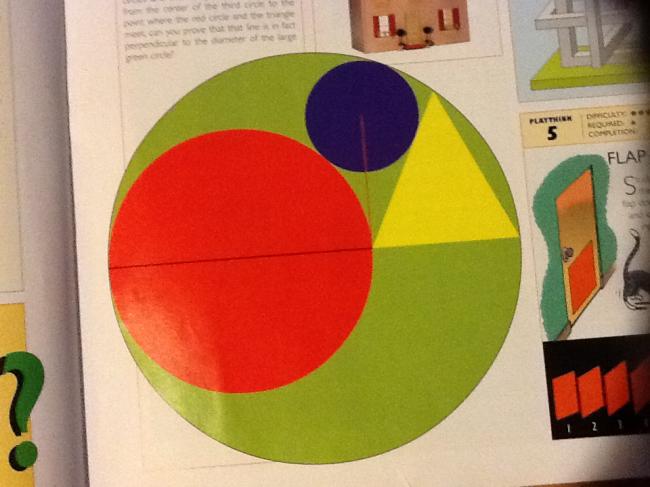
几年过去,我把这事几乎忘了。今年,朋友给我女儿送了一本对她来说相当超前的书,第一题就是个下马威(如照片),红圆的圆心在直径上,三角形为等腰三角形,底边与同一直径重合,蓝圆与红绿两圆及三角形相切。证明蓝圆圆心与图中交点连线与该直径垂直。又是思考良久,又是做不出。
这平面几何和数学其他分支不太一样,平时很少用到,以至于文革中“圆规直尺作图”被批判为套在工农兵手上的枷锁,“为什么不能用其他工具?”当年考大学,我数理化“铁人三项”全是自学的,结果强项数学居然得分最低,当时物理99,化学95.5,数学84,就是因为一道15分的平面几何题没能证出。
平时朋友问我数学,可谓无往而不胜,而如今在平面几何,居然连折两阵,这下给我敲响了警钟。以后女儿学平面几何时,老爸很可能帮不上忙,或者作用有限。送书(我不在乎“送输”)朋友的儿子将要进入高中,我就问他平面几何用什么书,随即买了一本。
书很快就到,由于惰性又赖了几个月,暑假开始到现在,学了一百多页。尽管尚未进入核心价值,但已觉得帮助不小。当初我学的是17本自学丛书,如今这美国人的书就活泼的多。某一章的引言是教你如何用指北针定位,还有一章有一页专门介绍木匠的作用。
第一个大吃一惊是“同位角相等”居然是条公理,无法证明的。原来我一向“记得”这是证明的定理,所以不太甘心,地铁上冥思苦想好几次,发现总有个绕不过的坎儿,最后只得作罢。
第二个大吃一惊是几何书居然介绍数学归纳法。我这个做排列组合的,对此理所当然的情有独钟,对于归纳法的三部曲可说是倒背如流。小时候读过一本归纳法(科普)“专著”,介绍过一些忽略第一或第二步所产生错误结论,还介绍过一个肯定很有名的例子,一个公式当K=1,2,3 。。。一直到一个很大的数还成立,然而再加一就不成立了。事隔多年,这个例子是不可能找到了,但书中居然给了一个同样令人惊讶的例子。一个圆上任取两个点,将其相连,将圆分为两部分。三点及连线分为4部分,四点8部分,5点16部分。6点。。。书把图画出,让读者自己仔细数,我数的结果是。。。31部分。这三部曲中的第三部从K到K+1,看上去是例行公事,实际上是万万不能省略的。
这本书有近800页,以我这蜗牛速度,到女儿进初中也应该可以学完了。









