| 中國古代數學 |
| 送交者: 天蓉 2022年04月25日13:32:35 於 [教育學術] 發送悄悄話 |
中國古代數學古代的東西方皆有早期數學的誕生和發展,可謂彼此獨立各有千秋。 1.古中國的算學
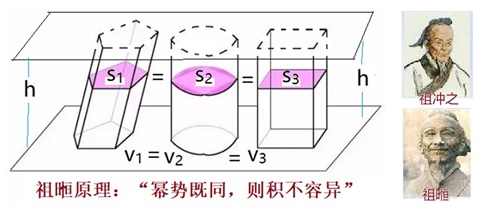
古希臘有阿基米德計算球體積的故事,中國的祖沖之和兒子祖暅也得到過同樣結果,但晚了約700年左右。不過他們使用的方法,即三國時代的劉徽首先提出、後來被稱之為“祖暅原理”的方法,卻比西方得到的同樣原理(卡瓦列里原理)早了一千多年。
祖暅原理說:“冪勢既同,則積不容異”,即如果所有等高處的截面積都相等,二立體的體積必相等。
實際上說穿了,中國古代數學的本質就是“計算”。祖沖之是中國古代最偉大的數學家,他的最大貢獻就是將圓周率的結果計算到了小數點後第7位,國際上因此稱圓周率為“祖率”,並建議將3月14日定為“祖沖之日”。祖沖之的天文成就包括計算和測量回歸日及月球繞地周期,其結果與現代數據相差無幾,由此月球上一個火山口,被學界命名為“祖沖之火山口”。
古中國與古希臘數學的另一區別是對數學發展的推動力。古希臘人視數學為愛好和遊戲,古中國獨尊文史輕視數理,因此數學發展的驅動力基本上只是“實用”。“實用是目的,計算為核心”。這也就是為什麼有人說中國古代並無“數學”,只有“算學”的原因。
因此,中國古代數學的主要特點是其算學特點。算學也有它先進發達的一面,並非完全沒有理論,中國古代數學也有不少密切聯繫實際的理論,比如與算法相關的推理證明等。中國古代的許多算法,稍加改變可以用到現代的電子計算機上。
古中國數學的機械化思想,與古希臘數學的公理化思想,是數學發展過程中的兩套馬車,都促進了數學的發展。古希臘以幾何為主,古中國多用代數方法,幾何比代數更容易公理化,代數比幾何更容易發展成機器算法。幾何直觀形象易於被眾人接受,代數在非專業人士眼中則顯得枯燥。可以說當時的兩者各具優缺點。
古希臘數學衰落而通過阿拉伯傳到歐洲的那段時期,正好是中國幾位數學家劉徽祖沖之等活躍的時候。這兩個分支在各自的跑道上獨立發展,沒有太大的關聯。
在羅馬帝國與歐洲中世紀,數學的自由精神受到限制,而中國古代數學卻在13世紀(宋朝)時達到了巔峰。
不過再到後來,情況又逐漸走向反面,中國的封建社會和中央集權遏制了學術的發展,學術水平非但不進步反而巨大倒退,文化專制和盲目排外使得數學及科學均逐漸落伍。
2. 韓信點兵--中國剩餘定理
“韓信點兵,多多益善”是一個成語,也涉及到中國古代一個著名的數學故事。秦末楚漢相爭時,韓信率1500名將士,但第一次戰後損傷了3、4百,於是,他急速點兵準備迎接下一場戰鬥。他的方法與眾不同別出心裁。他命令士兵每3人排一排,發現最後多了2名,如每5人排一排則多3名,7人排一排,又是多出2名。然後韓信立即得出了他的兵員數是1073名。
這個數學問題的學術版名字叫做“中國剩餘定理”,是我們中國古代數學貢獻於世界的最光輝一篇。享譽世界,對數論研究、密碼學及通俗如程序設計都有意義。
這道題最早出現在一千多年前的《孫子算經》中。
那只是當時一道不太起眼的叫做“物不知其數”的算術題:“今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二,問物幾何?”翻譯成現在使用的數學語言:一個數除以3余2,除以5余3,除以7余2,求這個數。比較聰明的小學生立刻能湊出來一個數:23。檢查一下也的確符合題目所給的3個條件。
我說23是湊出來的,因為23是很小的數!對這個簡單情況我們可以使用列舉法,
除3余2的數:2,5,8,11,14,17,20,23,26…… 除5余3的數:3,8,13,18,23,28…… 除7余2的數:9,16,23,30……
滿足這三個條件的共同數是“23”,所以便得到了答案。
不過眼尖的讀者也發現這個結果並不適合韓信點兵,兵數太少了!韓信的兵至少1000以上啊。不過這個問題有不止一個答案,事實上,答案(通解)可以寫成:23+3*5*7*t = 23+105t,其中t = 0, 1, 2……。由此可以得到在任何整數範圍問題的答案。例如,如果設t = 10,便得到了韓信的答案。
上面的分析雖然簡單,也可以悟出幾條此類問題的共同特點:
1,答案需要滿足3個條件,2,答案不止一個,可以加上被除數的公倍數的倍數。3,公倍數很重要。
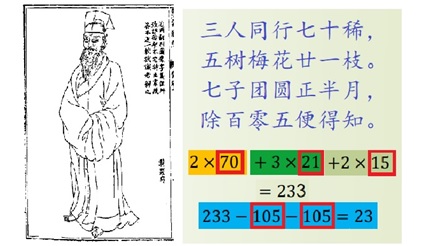
明朝有位數學家叫程大位,他用四句詩概括這個問題的解決方案:
為什麼70,21,15,105有如此神奇作用?70,21,15,105是從何而來?
這幾個數的性質:70除以3余1,被5,7整除,所以70a除以3余a,也被5,7整除;21余以5余1,被3,7整除,所以21b除以5余b,也被3,7整除;15除以7余1,被3,5整除,所以15c除以7余c,被3,5整除。而105則是3,5,7的最小公倍數。
總之來說:70a+21b+15c是被3除余a,被5除余b,被7除余c的數,這個數如果大於公倍數105,便逐次減去直到得到23。
因此,一個數學難題的意義是在於得到它的通解以及進一步的推廣。研究這個問題的主要的是一位宋朝數學家秦九韶,他才是對“物不知數”問題作出完整系統解答的人,載於1247年秦九韶的《數書九章》中,從而使這一問題變為了定理。再後來,《數書九章》由偉烈亞力在19世紀初譯為英文,德國數學王子高斯在1801年對此類問題提出最早的完整系統解法。
這個物不知其數的題目,推廣成“中國剩餘定理”是這麼說的:
中國剩餘定理成為數論中關於一元線性同餘方程組的重要定理,說明了一元線性同餘方程組有解的準則以及求解方法。
3. 古中國的“方程術”
上一節介紹的“韓信點兵”(物不知其數)問題,來自《孫子算經》。該書中還有很多有趣的數學問題,比如雞兔同籠就是一個幾乎人人皆知的著名數學題。“雞兔同籠,頭共10,足共28,雞兔各幾隻?”,設雞x,兔y:x+y=10, 2x+4y=28, 加減再消元,便可求得答案為4兔6雞。這個問題非常簡單,但卻代表了代數中的一大類問題:n元一次方程組。具體對這道雞兔同籠問題,就是解一個2元一次方程組。
二元(n=2)的意思是有x和y兩個變量,“一次”是說只包含變量的1次項,說明方程是線性的。本題的方程組中有兩個方程,才能解出兩個變量。
中國古代數學著作中比較有名的,除了6世紀的《孫子算經》之外,還有早好幾百年的《九章算術》。就成書的年代及篇幅而言,它們可以與古希臘數學相媲美。但中國數學書的特點是演繹和定理比較少,用現在的標準看起來,不像教科書,像是習題集和答案,再加上了有關解題方法的一些敘述。這是因為中國古代數學輕演繹重應用的原因。另外就是古希臘數學的重點是幾何,古中國數學有更為濃郁的代數色彩,更像是7-8世紀的印度或阿拉伯的數學。
在《九章算術》中,第八章“方程”的第一道題目,就是解一個三元一次方程組(圖1.7.5)。三個未知數,比雞兔同籠問題多了一元,更為複雜一點。
圖5:《九章算術》“方程術”中的代數題(YouTube視頻)
我們可以用現有的代數方法解這道題:令 x, y, z 分別代表上等稻、中等稻和下等稻各1捆所能打出的稻米斗數,然後列出如圖1.7.5右所示的三元一次聯立方程組,經過分離變量和消元過程,便能得到圖1.7.5右下角所示的x, y, z 數值。
張蒼的年代稍後於阿基米德,大約是公元前200年左右的人士,陽武(今河南原陽)人。他不僅是西漢時期“以善算命世”的數學家兼天文學家,又是西漢的開國功臣,並且官至丞相十幾年,他的政治聲譽大於科技的。在數學方面,他是《九章算術》的作者和編輯者之一。
《九章算術》中,對於開平方術、開立方術,敘述非常詳盡,在當時也是很先進的方法。“方程術”與“開方術”相結合,後來發展了高次代數方程的“天元術” ,可以解出二項二次方程、二項三次方程,或更高次的方程,在數學的發展中也有重要地位。此是後話不表。
圖7:用符號表示的“天元術”的3次方程
4. “嘗擬雄心勝丈夫 ”
嘗擬雄心勝丈夫,這句詩出自於中國清朝一位女數學家王貞儀。
你可能沒聽過這位女科學家,但她在世界上卻有一定的知名度:金星上有一個以她命名的撞擊坑,還有一顆小行星也以她命名。
圖8:有關王貞儀的書和視頻
王貞儀(1768~1797),字德卿,生於江寧府(今江蘇南京),祖父宣化太守王者輔熱愛讀書,據說有藏書七十五櫥,且精通曆算,著述頗豐,父親王錫琛科舉不中,轉而學醫,精通醫術。出身於如此家庭,自小聰明好學喜愛讀書的王貞儀,從祖父學習天文,從祖母學詩詞,父親則教她醫學、地理和數學。後來她又隨同祖母和父親去過北京、陝西、湖北、廣東和安徽等地,遊覽名勝古蹟,見聞頗多,也接觸到不少社會實際。25歲時和安徽宣城的一個叫詹枚的青年結了婚,沒有孩子,並且不幸於29歲時英年早逝。
王貞儀只活了短短的29年,但卻留下不少著作。
數學著作有《西洋籌算增刪》、《重訂策算證訛》、《象數窺余》、《術算簡存》、《籌算易知》、《勾股三角解》等。
文學作品《德風亭詩鈔》和《德風亭集》。
天文學書籍:《歲差日至辯疑》、《盈縮高卑辯》、《經星辯》、《黃赤二道解》、《地圓論》、《地球比九重天論》、《歲輪定於地心論》、《日月五星隨天左旋論一、二、三》、《月食解》
從她遺留下來的著作可以看出,她是一位從事天文和籌算研究的女數學家。
據說她曾積極宣傳闡釋哥白尼的日心說,這在當時十分難能可貴。她用自己的獨立見解來詮釋“天圓地方”,並對日月食的成因做出了通俗易懂的解釋。她還對歲差的成因、測量和計算做出貢獻。
她寫過一本介紹西方“算籌”的書。算籌是一種棒狀的計算工具,其作用類似算盤。應用“算籌”進行計算的方法叫作“籌算”。17世紀初葉,英國數學家納皮爾發明了一種算籌計算法,明末介紹到我國,也稱為“籌算”。清代著名數學家梅文鼎、戴震等人曾加以研究,還短暫地形成了一個安徽數學學派。王貞儀祖籍安徽,當年是這一學派的主要成員之一。她研究由西洋傳入中國的這種籌算,並且寫了三卷書向國人介紹。王貞儀思想開放,主張取中西算法之優點。對此,她在《勾股三角解》中有一段十分精彩的論述:“中西固有所異,而亦有所合。然其法理之密、心思之微,而未可以忽視。夫益知理求是,何擇乎中西?唯各極其兼收之義。”
王貞儀酷愛天文,喜歡自己動手,她用屋頂橫梁上懸掛的水晶燈當做太陽、小圓桌當做地球、圓形的鏡子當作月亮。根據天文學原理,她一邊移動這三個物體,一邊不斷地觀察它們的相對位置和造成的現象,終於弄清了日月食的原理。她寫了《月食解》一文,精確地闡釋了月食發生的時間、食分深淺等知識,語言淺顯直白,還有配圖。王貞儀在她的另一部著作《地圓論》中,揭示了“相對空間位置的概念”,即宇宙沒有上、下、正、反之分,以此而批駁流傳了數千年的天圓地方之說。
她頗有文才,寫詩填詞懂繪畫。“峰勢長江矗,濤飛天外聲。潛虬能護法,徵士獨留名。”、“始信鬚眉等巾幗,誰言兒女不英雄?”是她的詩句。 ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× 本人的科普視頻:YouTube: 天文航天:“談天說地” https://www.youtube.com/playlist?list=PL6YHSDB0mjBLmFkh2_9b9fAlN7C4618gK 趣味數學:數學大觀園 https://www.youtube.com/playlist?list=PL6YHSDB0mjBJifi3hkHL25P3K9T-bmzeA 也發在微信公眾號“天舸”上(微信號:gh_e01fc368fe31):
長按/掃一掃二維碼,敬請關注我的微信公眾號“天舸” ! ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× |
|
|
 | |
|
 |
| 實用資訊 | |
|
|
| 一周點擊熱帖 | 更多>> |
| 一周回復熱帖 |
| 歷史上的今天:回復熱帖 |
| 2021: | 茅于軾:剩餘價值理論是完全錯誤的 | |
| 2020: | 他們用生命托住世界 | |
| 2020: | 包皮環割和蓮花清瘟 | |
| 2019: | How to measure return | |
| 2019: | 宋詩解(3) | |
| 2018: | 彭運生談藝錄(208) | |
| 2018: | 科學家趣聞 | |
| 2017: | 胖子,這提出了重朔中華民族知識產權及 | |
| 2017: | 中大暑假課程 助中小生研究 | |